作者:水奈樾 人工智能爱好者
博客专栏:http://www.cnblogs.com/rucwxb/
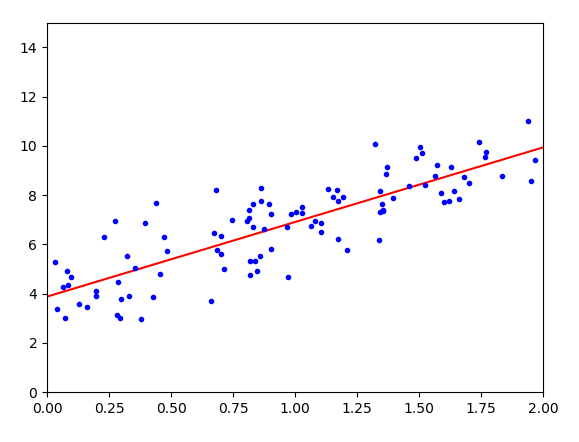
一、Linear Regression
线性回归是相对简单的一种,表达式如下
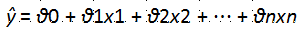
其中,θ0表示bias,其他可以看做weight,可以转换为如下形式
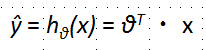
为了更好回归,定义损失函数,并尽量缩小这个函数值,使用MSE方法(mean square equal)
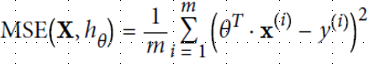
缩小方法采用梯度下降法,即不断地向现在站立的山坡往下走,走的速度就是学习速率η(learning rate),太小耗尽计算资源,太大走过了山谷。
(1)Normal Equation
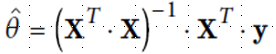
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
# 数据集
X = 2*np.random.rand(100, 1)
y = 4+3*X+np.random.randn(100,1)
# X每个元素加1
X_b = np.c_[np.ones((100,1)), X]
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
# 训练
lin_reg = LinearRegression()
lin_reg.fit(X, y)
print(lin_reg.intercept_, lin_reg.coef_)
# 测试数据
X_new = np.array([[0],[2]])
X_new_b = np.c_[np.ones((2,1)), X_new]
y_predict = X_new_b.dot(theta_best)
print(y_predict)
# 画图
plt.plot(X_new, y_predict, "")
plt.plot(X, y, "b.")
plt.axis([0,2,0,15])
plt.show()
(2)Batch Gradient Descent
基本算是遍历了所有数据,不适用于数据规模大的数据
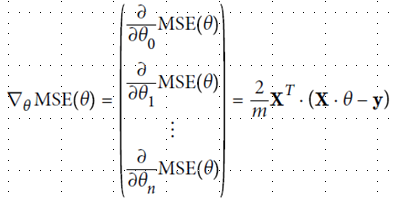
# BGD梯度下降
eta = 0.1
n_iterations = 1000
m = 100
theta = np.random.randn(2,1)
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta*gradients
print(theta)
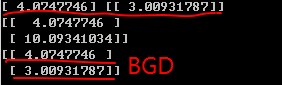
可以看出,结果是差不多的
(3)Stochastic Gradient Descent
可以避免局部最优结果,但是会震来震去。为了防止这种震荡,让学习速率η不断减小(类似模拟退火)
# SGD梯度下降
m = 100
n_epochs = 50
t0, t1 = 5, 50 # η初始值0.1
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2,1) # random initialization
for epoch in range(n_epochs):
for i in range(m):
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch * m + i)
theta = theta - eta * gradients
print(theta)
# sklearn 提供了SGDRegressor的方法
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=50, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())
print(sgd_reg.intercept_, sgd_reg.coef_)
(4)Min-batch Gradient Descent
使用小批随机数据,结合SGD与BGD优点
以下是各种方法对比

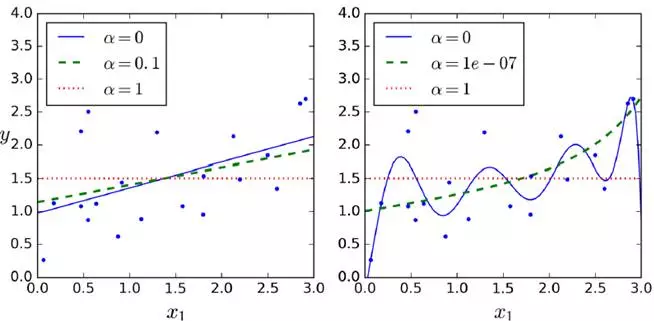
二、Polynomial Regression
但有的时候,y本身是由x取平方所得,无法找出来一条合适的线性回归线来拟合数据,该怎么办呢?
我们可以尝试将x取平方,取3次方等方法,多加尝试。
三、误差分析四、防止过拟合
用惩罚系数(penalty),即正则项(regularize the model)
(1)岭回归ridge regression
控制参数自由度,减少模型复杂度。所控制的α=α ,越大控制结果越强
,越大控制结果越强

优势:直接用公式可以计算出结果
1 from sklearn.linear_model import Ridge
2 ridge_reg = Ridge(alpha=1, solver="cholesky")
3 ridge_reg.fit(X, y)
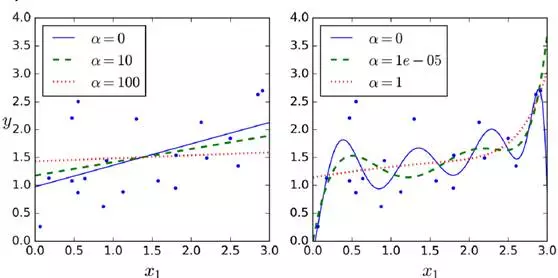
(2)Lasso Regression(least absolute shrinkage and selection operator regression)
正则化项同ridge regression不同,正则化的控制更强
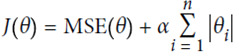
1 # Lasso Regression
2 from sklearn.linear_model import Lasso
3 lasso_reg = Lasso(alpha=0.1)
4 lasso_reg.fit(X, y)
5 lasso_reg.predict([[1.5]])
对于高阶degree regularize尤为明显,是一个sparse model,很多高阶参数项成为了0
(3)Elastic Net(一般推荐使用)
相当于ridge和lasso regression的结合,用超参数r来控制其平衡
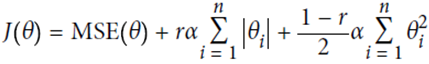
1 # Elastic Net
2 from sklearn.linear_model import ElasticNet
3 elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
4 elastic_net.fit(X, y)
(4)Early Stopping
找到开始上升的点,从那里停止(整体找到,取最优的)
from sklearn.base import clone
sgd_reg = SGDRegressor(n_iter=1, warm_start=True, penalty=None,
learning_rate="constant", eta0=0.0005)
minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled, y_train) # continues where it left off
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
val_error = mean_squared_error(y_val_predict, y_val)
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = clone(sgd_reg)
五、Logistic Regression
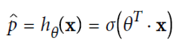
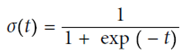
(使用sigmod函数,y在(0,1)之间)
定义cost function,由于p在(0,1)之间,故最前面加一个符号,保证代价始终为正的。p值越大,整体cost越小,预测的越对
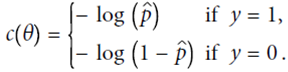
即
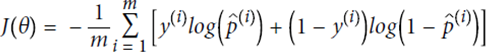
不存在解析解,故用偏导数计算
以Iris花的种类划分为例
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
print(list(iris.keys()))
# ['DESCR', 'data', 'target', 'target_names', 'feature_names']
X = iris["data"][:, 3:] # petal width
y = (iris["target"] == 2).astype(np.int) # 1 if Iris-Virginica, else 0
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X, y)
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
# estimated probabilities for flowers with petal widths varying from 0 to 3 cm:
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "", label="Iris-Virginica")
plt.plot(X_new, y_proba[:, 0], "b--", label="Not Iris-Virginica")
plt.show()
# + more Matplotlib code to make the image look pretty
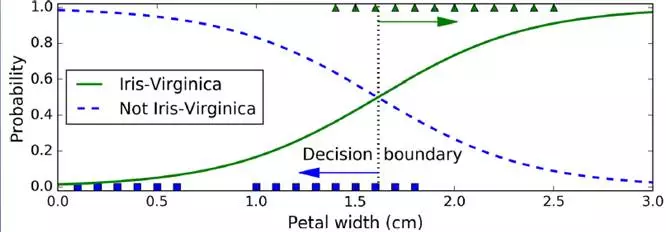
六、Softmax Regression
可以用做多分类

使用交叉熵
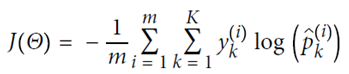
X = iris["data"][:, (2, 3)] # petal length, petal width
y = iris["target"]
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10)
softmax_reg.fit(X, y)
print(softmax_reg.predict([[5, 2]]))
# array([2])
print(softmax_reg.predict_proba([[5, 2]]))
# array([[ 6.33134078e-07, 5.75276067e-02, 9.42471760e-01]])
公众号后台回复关键词学习
回复 人工智能 揭开人工智能的神秘面纱
回复 贝叶斯算法 贝叶斯算法与新闻分类
回复 机器学习 R&Python机器学习
回复 阿里数据 阿里数据系列课程
回复 Python Python机器学习案例实战
回复 Spark 征服Spark第一季
回复 kaggle 机器学习kaggle案例
回复 大数据 大数据系列视频
回复 数据分析 数据分析人员的转型
回复 数据挖掘 数据挖掘与人工智能
回复 机器学习 R&Python机器学习
回复 阿里数据 阿里数据系列课程
回复 R R&Python机器学习入门
