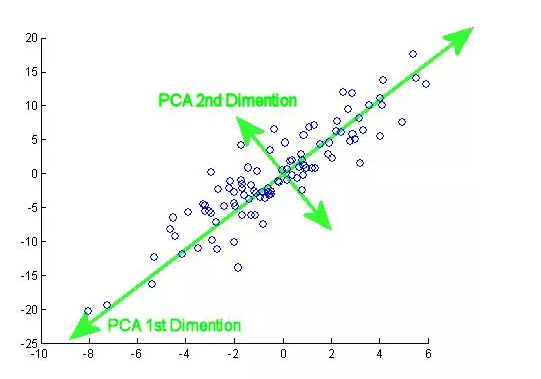
本文聊聊主成分分析(principal component analysis, PCA),首先谈谈协方差。
方差和协方差是用来衡量一系列点在它们的重心或均值周围的分散程度的。方差可以标度这些点在一个维度的偏差, 而协方差是用来衡量一个维度是否会对另外一个维度有所影响的。协方差对两个维度进行衡量,进而查看这两个维度之间是否有关系。显然,某个维度跟自身之间的协方差就是方差。
协方差计算公式如下:
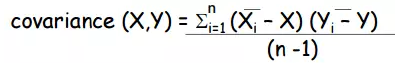
如果数据集中的样本是d维的,(x1, x2, ..., xd),则可以计算(x1,x2),(x1,x3),...,(x1,xd), (x2,x3), ..., (x2,xd),(x3,x4),...,(x d-1,xd)之间的协方差,共d(d-1)个协方差,由于对称性,只需计算d(d-1)/2个协方差。此时,需要计算(x1,x1), (x2,x2), ...,(xd,xd)共d个方差。
上面的协方差和方差组合起来,可以构成协方差矩阵,形式如下:
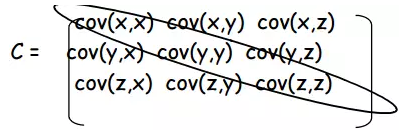
其中对角线上的是方差。协方差矩阵关于对角线呈现出对称分布。矩阵的大小跟样本自身维度有关,如果样本是d维的,则相应的矩阵就是d×d维的。
为清晰明了起见,下图给出了正负协方差的示例,左图具有正的协方差,右图具有负的协方差。
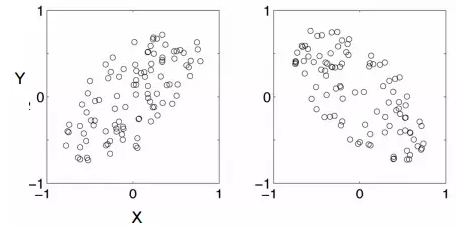
协方差为正,说明两个变量变化趋势相同,一个变量增长另一个变量也增长,反之亦然。协方差为负,说明两个变量变化趋势相反,一个变量减小另一个变量增长,该变量增长时另一个变量减小。如果协方差为零,则两个变量之间并不会相互影响,而是相互独立。
主成分分析(principal components analysis,PCA)是一种可以简化数据集的技巧。这种方法通过线性变换将原数据映射到新的坐标系统中,使得映射后的第一个坐标上方差最大(第一个主成分),第二个坐标上的方差第二大,以此类推。主成分分析可以通过省去后面的主成分,来达到降维的目的。
下面来看一个例子。考虑三维样本点。
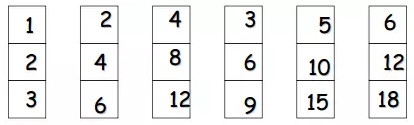
仔细观察,不难发现,这些元素都是有关联的,可以看成同一个元素,只是相差缩放因子。
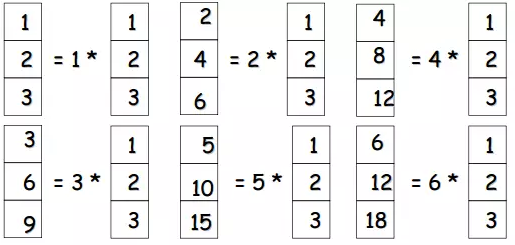
如此一来,可以减小存储空间,现在只需保存一个向量,六个缩放因子。
接下来看看几个解释。本例中,所有点都在一条线上,意即所有点都在原空间中的一维子空间中。
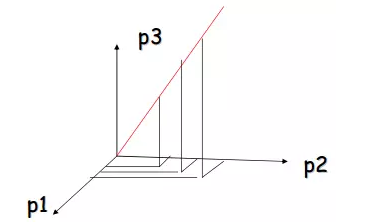
将这条线作为其中一个坐标,可以得到一个新的坐标系,如下图所示。
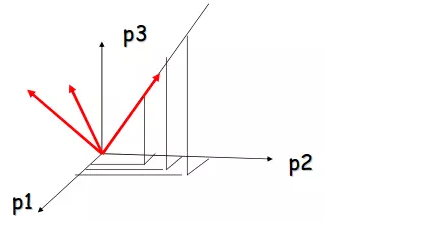
在新坐标系中,每个点只有一个坐标不为零,此时只需要存储这条线的方向和每个点的非零坐标。
给定新的样本点集合,如何判断该集合是否可以像上述例子那样加以压缩呢?这需要分析样本点之间的相关性,而且主成分分析就是解决这个问题的。
通过计算协方差矩阵的特征值和特征向量,可以发现最大特征值对应的特征向量跟数据集中具有最强关联的维度相一致。这就是主成分,主成分分析是一种比较有用的统计方法,在人脸识别和图像压缩领域中得以应用,也可以在高纬数据中发现模式。
主成分分析一般流程如下:
给定
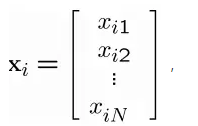
计算均值向量
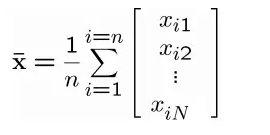
得到一个矩阵
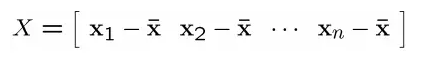
这里值得注意的是,减去均值其实就是将坐标系平移。
进而得到协方差矩阵
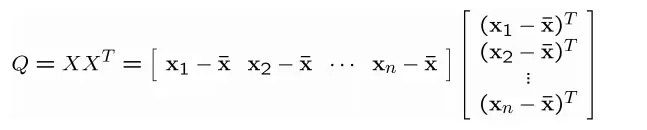
值得注意的是,Q是一个方阵,而且是对称的,通常维度比较大,在计算机视觉中,这里的矩阵维度就是一张图像中像素个数。
原始数据中的每个样本都可以写成下述形式:
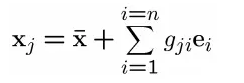
其中ei是矩阵Q非零特征值对应的特征向量。值得注意的是,特征向量e1,e2,...,en可以张成特征空间,这些向量相互正交。gji是xj在新张成空间中的坐标
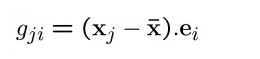
将x表示成e1,e2,...,en的组合并不改变数据的维度,但是,如果样本点高度相关,则新坐标系中样本点的坐标会为0或者接近0。值得注意的是,这意味着可以将原始样本点压缩到低维线性子空间中。
将特征向量按特征值从大到小排序,
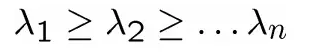
并且假设
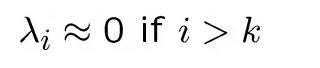
则
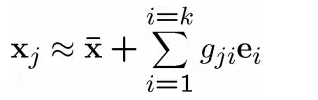
其实,主成分就是输入空间中具有最大方差的方向,并且跟协方差矩阵的主特征向量相同。