

机器学习中对目标函数进行优化时,通常需要一些优化算法。其中比较常用的算法都是基于梯度下降法或牛顿法或者相关变形算法。
首先来看下梯度下降过程中每次迭代的公式,
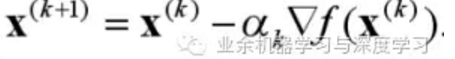
其中αk是一个标量,称为步幅或者学习率。梯度下降法的收敛速度高度依赖于学习率,如果步幅较小,则迭代比较"费劲",如果步幅较大,则调整过程呈现Z字形或称调整过程比较曲折。如下图所示(左边学习率较小,右边学习率较大):

谈到梯度下降,不免要提到最速梯度下降,最速梯度下降对应的梯度即为使得目标函数下降最快的方向。迭代过程中需要一定的终止条件,那么最速梯度下降如何停止迭代呢?下面即为几个停止迭代的标准:

当然,也可以通过指定终止迭代次数来终止。
梯度下降法根据每次迭代所依赖的样本个数又可以分为以下三种:
随机梯度下降法:
每次更新系数只利用一个样本。
优点:在大规模数据集上收敛速度更快,每次迭代计算量较小;
缺点:
• 一直反弹,除非缩减学习率;
• 不易达到高准确率;
• 收敛不容易定义;
• 多数情形下二阶方法不work;
关键代码如下:
for i in range(nb_epochs):
np.random.shuffle(data)
for example in data:
params_grad = evaluate_gradient(loss_function, example, params)
params = params - learning_rate * params_grad
批梯度下降法:
每次更新系数利用全部样本点。
优点:
• 简单条件下能够保证收敛到局部最小值;
• 有很多技巧可以提高学习速率
缺点: 大规模数据集比较“痛苦”,每次迭代计算量比较大;
关键代码如下:
for i in range(nb_epochs):
params_grad = evaluate_gradient(loss_function, data, params)
params = params - learning_rate * params_grad
相对以上两种梯度下降法,还有一种比较折衷的梯度下降法即mini-batch 梯度下降法:
即将整体样本集分成若干个小批。
关键代码如下:
for i in range(nb_epochs):
np.random.shuffle(data)
for batch in get_batches(data, batch_size=50):
params_grad = evaluate_gradient(loss_function, batch, params)
params = params - learning_rate * params_grad
下面谈谈牛顿法。
牛顿法既利用一阶导数,又利用二阶导数,这种方法对于初始点接近最小值时效果较好。牛顿法假设目标函数在局部是二阶函数,并且相应的海森矩阵是正定的,海森矩阵比较难计算,而且计算复杂度较高。
注:
高斯-牛顿法是牛顿法的一种变形算法,这种算法不需要计算海森矩阵,计算复杂度是O(d^2),其中d为特征个数。
L-BFGS(Limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS))是一种quasi-Newton算法,这种算法需要计算目标函数的海森矩阵的近似。L-BFGS算法避免了存储Hessian矩阵的一系列近似,这方便了将其用于高维情形。在L-BFGS中,基于前面的m步来保存曲率信息,并利用其来寻找新的搜索方向。再解释下,这种算法不计算也不存储hessian矩阵的信息,而是存储空间变换和梯度变化信息。
共轭梯度下降法依赖于共轭方向,如果u^T A v = 0 ,则称向量u和向量v共轭,其中A是矩阵。这种方法中移动时朝着跟最速梯度方向互为共轭方向的方向移动。