大家可以参考这篇博客对朴素贝叶斯的介绍，在这里主要将朴素贝叶斯分类和朴素贝叶斯的参数估计进行介绍，大家注意，朴素贝叶斯不等同于贝叶斯估计；
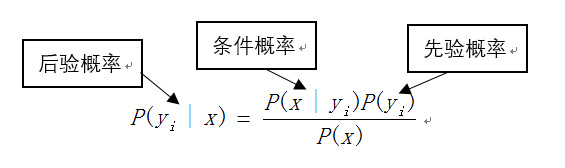
一开始我们不知道某一目标事件发生的真实状态，我们只能够估计出某一事件发生的先验概率，随着得到的信息特征或证据越来越多，我们可以通过给定的信息来判断某一事件发生的后验概率；朴素贝叶斯算法有以下几点优缺点：
1、 优点：简单、快速、有效
能处理好噪声数据和缺失的数据
需要用来训练的例子相对较少，但同样能处理好大量的例子
很容易获得一个预测的估计概率值
2、 缺点：
依赖于常用的错误假设，即所有的特征属性拥有一样的重要性和独立性
应用在含有大量数值特征的数据集时并不理想
概率的估计值相对于预测的类而言更加不靠谱
下面说一说连续变量的处理，针对连续变量我这里接触到两种处理方法
a) 假设某一特征属性服从正态分布，计算出均值和方差，即可得到正态分布的密度函数，算出某一点的密度函数的值
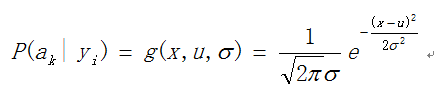
因此只要计算出训练样本中各个类别中此特征项划分的各均值和标准差，代入上述公式即可得到需要的估计值。
a) 将连续变量离散化，计算不同区间的概率值代替改点的概率值
下面讲一个对连续变量进行朴素贝叶斯分类的例子
本例摘自维基百科，关于处理连续变量的另一种方法。
下面是一组人类身体特征的统计资料。
性别 身高（英尺） 体重（磅） 脚掌（英寸）
男 6 180 12
男 5.92 190 11
男 5.58 170 12
男 5.92 165 10
女 5 100 6
女 5.5 150 8
女 5.42 130 7
女 5.75 150 9
已知某人身高6英尺、体重130磅，脚掌8英寸，请问该人是男是女？
根据朴素贝叶斯分类器，计算下面这个式子的值。
P(身高|性别) x P(体重|性别) x P(脚掌|性别) x P(性别)
由于身高、体重、脚掌都是连续变量，不能采用离散变量的方法计算概率。而且由于样本太少，所以也无法分成区间计算。怎么办？
这时，可以假设男性和女性的身高、体重、脚掌都是正态分布，通过样本计算出均值和方差，也就是得到正态分布的密度函数。有了密度函数，就可以把值代入，算出某一点的密度函数的值。
比如，男性的身高是均值5.855、标准差0.187的正态分布。所以，男性的身高为6英尺的概率的相对值等于1.5789。
#朴素贝叶斯算法
#导入数据，读取复制后剪切板的数据
> w<-read.table("clipboard",T)#计算身高分别为男性、女性的均值、标准差
> u
[,1] [,2]
男 5.8550 0.1871719
女 5.4175 0.3118092#计算身高6英尺的概率密度函数
> (P_height<- dnorm(6,mean(w[w$性别=="男",2]),sd(w[w$性别=="男",2])))
[1] 1.578883#计算身高6英尺、体重130磅，脚掌8英寸为男性的概率
> p<-dnorm(6,mean(w[w$性别=="男",2]),sd(w[w$性别=="男",2]))*
+ dnorm(130,mean(w[w$性别=="男",3]),sd(w[w$性别=="男",3]))*
+ dnorm(8,mean(w[w$性别=="男",4]),sd(w[w$性别=="男",4]))
> p
[1] 1.239414e-08#计算身高6英尺、体重130磅，脚掌8英寸为女性的概率
> q<-dnorm(6,mean(w[w$性别=="女",2]),sd(w[w$性别=="女",2]))*
+ dnorm(130,mean(w[w$性别=="女",3]),sd(w[w$性别=="女",3]))*
+ dnorm(8,mean(w[w$性别=="女",4]),sd(w[w$性别=="女",4]))
> q
[1] 0.001075582> q/p
[1] 86781.46因此可以判断为女性。
接下来说一说当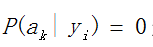
怎么办？
当某个类别下某个特征项划分没有出现时，就是产生这种现象，这会令分类器质量大大降低。为了解决这个问题，我们引入Laplace校准，它的思想非常简单，就是对没类别下所有划分的计数加1，这样如果训练样本集数量充分大时，并不会对结果产生影响，并且解决了上述条件概率为0的尴尬局面。在后面我会继续讲，这就是朴素贝叶斯参数估计的贝叶斯估计。
朴素贝叶斯法的参数估计
朴素贝叶斯法的参数估计有最大似然估计和贝叶斯估计，贝叶斯估计可以对上述所说的
最大似然估计：
浩彬老撕在探寻数理很通俗易懂的讲了一个例子。
假如一个长发飘飘的人从你面前一闪而过，下意识的你会判断这是个女生；
这就是一个极大似然估计思考的过程，让我们简单回顾一下：
你看到了一个人，并且看到ta是长头发的。尽管这个同学可能是男的，也可能是女，但是你根据经验判断，女生的长头发的可能性有95%，男生长头发的可能性只有4%，于是，你根据这个可能性做出了判断，她是一个女生。没错，这种按照可能性最大的猜测正是极大似然估计的思想。
超模君在这里例举了一个袋子里摸球的例子，并且给出了具体的分析思路。
我们假设袋中白球的比例是p，那么黑球的比例就是1-p。而每抽一个球出来，在记录完颜色之后，我们把抽出的球放回了袋中并摇匀：
因此每次抽出来的球的颜色这一事件相互独立并且服从同一分布（即期望和方差相同）。
事实上，p是有很多种分布的。而根据我们所谓的常识：在这100次抽取的过程中，出现了70次是白球，那我们肯定不会认为白球：黑球 = 5:5 ，而是倾向于认为白球：黑球 = 7:3。
现在，我们把一次抽出来球的颜色称为一次抽样。而在上面的题目的在100次抽样中，我们将70次是白球，30次是黑球的概率记为P(样本结果 | M)，每次抽出来的球是白色的概率记为p。如果第一次抽样的结果记为x1，第二次抽样的结果记为x2，……那么样本结果= (x1，x2，...，x100)。于是：
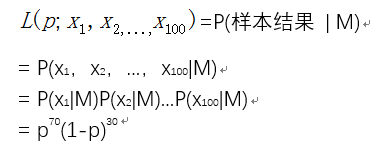
显然，当p=0或者1时，P(样本结果|M)=0，因此在p∈（0，1），P(样本结果|M)会有一个极大值（或极小值）。
而极大似然法就是令样本出现的概率最大，进而估计整体的模型参数。
那么，p在取什么值的时候，P(样本结果|M)的值最大呢？
很简单，只需将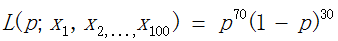
对p求导，并令其等于零，即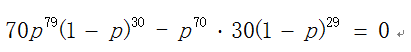
于是我们便可以得到p=0.7，即白球：黑球=7:3
再回到浩彬老撕这里来，
总结一下极大似然估计的一般步骤：
i. 根据概率密度函数写出似然函数；
ii. 对似然函数取对数；
iii. 对对数似然函数求导；
iv. 解方程，求得参数Θ；
极大似然估计讲了这么多，下面我们讲讲在朴素贝叶斯法中，用极大似然估计来求得先验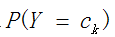概率
和条件概率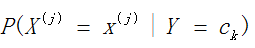
贝叶斯估计
这里我们就来讲讲上面所说的遇到条件概率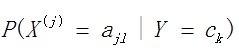
为0时的处理
用极大似然估计可能出现一个特征值得条件概率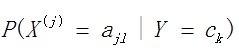为0的情况，这时会影响到后验概率的计算结果，使分类结果产生偏差，贝叶斯估计可以很好的解决该问题，贝叶斯估计引入Laplace校准，此时先验概率为
在naiveBayes()函数中可以通过laplace 参数来设置，默认情况下为0.
当laplace =0时，即为极大似然估计。
总结一下，主要讲了连续特征属性的两种处理办法，还有两种参数估计，一种是极大似然估计，另一种就是当条件概率为0时我们用到的贝叶斯估计。
朴素贝叶斯分类中假设所有特征变量都是条件独立的，如果它们之间存在概率依存关系，模型就变成了贝叶斯网络，有时间再继续学习整理。
