前言
欢迎来到“每天进步一点点2015”微信公众号，从本期开始，我们将给各位网友分享有关数据挖掘的理论与实战知识，实战部分将结合Python和R语言完成模型的落地。在这一期，我们将从统计模型中的回归开始入手，回归堪称是经典中的经典，很多现实问题都可以通过回归思想来解决。
从有监督、无监督和半监督的角度来看，回归其实是有监督的算法模型之一，反映的是根据某些已知变量(解释变量或自变量)去预测某个未知变量(被解释变量或因变量)。例如根据国民生产总值，预测人口的失业率；根据房屋的面积，朝向，交通状况等信息，预测房价；根据田地的面积，施肥状况，稻谷的品种，预测粮食产量等。你会发现，对于类似数值型的因变量预测，我们就可以借助于回归来完成。关于回归有很多种类，如多元线性回归、岭回归、Lasso回归等，本期开始，我们就介绍多元线性回归，后面也会分享到岭回归和Lasso回归。
多元线性回归
对多元线性回归模型有所了解的朋友，都知道因变量y与自变量X之间存在某种线性组合。 例如，现在手上有n个观测，p+1个变量，其中p个变量是自变量，1个变量是因变量，即如下方所示：
如上面所说的某种线性组合，指的是因变量y应该可以用自变量X来表示，并且它们之间是存在线性关系，即：
它们分别代表的是多元线性回归模型的偏回归系数和误差项。为了书写的方便，可以将回归模型的方程式写成：
极大似然估计
既然我们知道了多元线性回归模型中y与X的组合关系，那接下来关心的就是如何求出模型的偏回归系数。由于误差项是服从正态分布的，而误差项又是关于偏回归系数的表达式，即
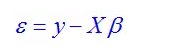
首先来看一下正态分布的概率密度函数：
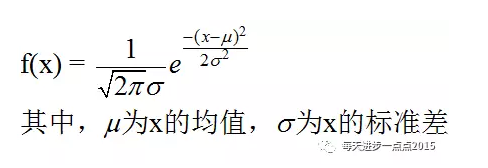
其次，根据该密度函数，可以将误差项的概率密度函数表示为：
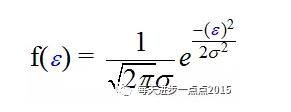
最后，我们可以这样理解，如果已知了X的观测和偏回归系数的值，那么就可以求得y值的概率值，即：
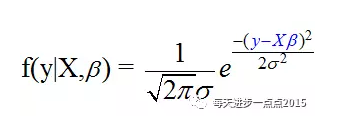
上面的理解只是由结果往前推断，但现在的问题是，不知道偏回归系数。上式反应的是计算y的条件概率，如果概率值越大，则说明预测出来的y会越接近于真实的y，所以，现在的问题就变成了计算概率的最大值。根据，观测之间的y是独立的假设，我们可以对其构造极大似然函数，即：
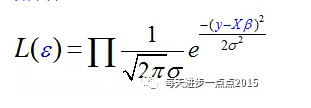
为了求解的方便，我们在等式两边取对数：
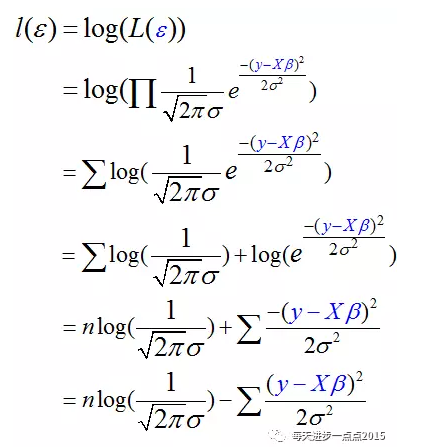
由于等式右边的前半部分是一个常数，而后半部分是一个负值，所以求解似然函数的极大值问题就转换成了求
最小二乘法
根据上面的极大似然函数的推导可知，要实现最优化问题的解决，就是求解误差平方和最小。这也很容易理解，即要想求得合理的偏回归系数，得到回归模型，就要保证该模型尽可能的拟合好真实的数据，而是否很好的拟合，不就是用误差来度量吗？误差越小，则预测的越接近于现实，否则就越偏离现实。接下来，我们就借助于最小二乘法的思想再来推导如何求得偏回归系数。
在推导之前，需要了解一些基本的线性代数知识，具体在下面给出：
向量的平方和
矩阵乘法的转置
矩阵的偏导数
求解偏回归系数的推导：
要想求得上面目标函数的最小值，可以通过求偏导数，然后使偏导数为0即可：
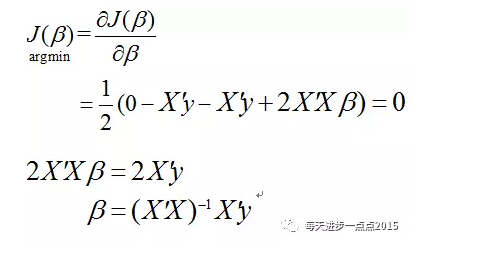
梯度下降法
根据上面的推导就可以得到多元线性回归模型的偏回归系数了。如果你也一步步的推导一遍，我相信对你理解多元线性回归模型是有一定的帮助的。但是，上面的普通最小二乘有一个小小的瑕疵（这个瑕疵发生的概率还是非常小的），并不能确保方阵X’X是可逆的，即X’X的行列式一定不为0，如果自变量之间存在高度共线性的话，那就会导致X’X是不可逆。这里，我们再分享一种利用“梯度下降”的方法实现偏回归参数的求解，该方法就可以很好的避免上面的瑕疵。
我们知道，目标函数
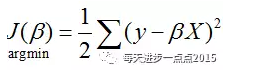
是关于偏回归系数的二次函数，且开口向上，即凸函数，那这样的目标函数就会存在极小值。所以，我们就可以对每个偏回归系数求偏导数，而偏导数据梯度的概念：
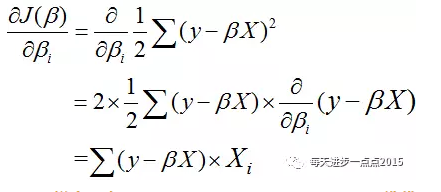
那梯度下降中的“下降”是什么意思呢？其实就是指迭代，每迭代一次，就是一次下降的过程，这个过程，就是为了找到目标函数的极小值，如下面的形象图示：
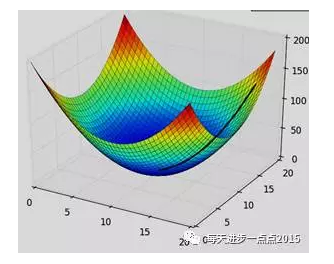
这种下降的迭代，可以用下面的公式表示：
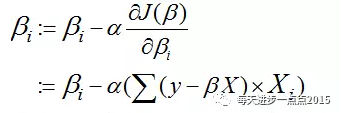
注意，这里的步长既不能太小，也不能太大，如果太小的话，会导致迭代次数暴增，降低算法的运行效率，加大运行的时间成本和运行空间；反之容易跨过极小值，无法达到全局最优。
模型的显著性检验
关于“梯度下降法”的介绍属于线性回归中的知识的扩展，我们还是把重点回归到最小二乘法。通过最小二乘法我们可以得到模型的偏回归系数，但计算得到系数就一定能够保证模型是OK的吗？这里还需要对模型的显著性进行必要的检验，而模型显著性检验的假设条件为：
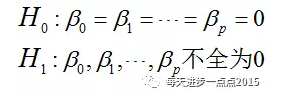
我们先从下面这张图来理解一下几个离差平方和的概念：
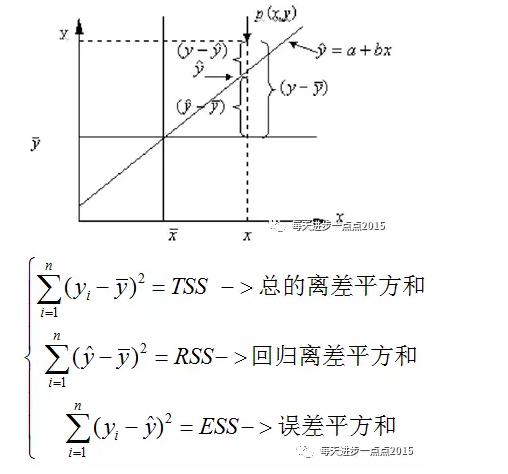
上面的三种离差平方和，存在这样的等式关系：TSS=RSS+ESS。实际上，TSS是固定，而ESS和RSS是跟模型的预测值有关的，如果模型拟合的越好，则误差平方和(ESS)应该越小，对应的RSS越大。所以，根据这两个离差平方和就可以构造模型检验的统计量F：
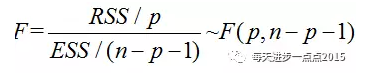
其中，p和n-p-1为RSS和ESS的自由度。当我需要检验模型是否OK的时候，只需要将计算出来的统计量F与理论的值作对比，如果统计量F值大于理论的临界值，则认为可以拒绝原假设H0，即接受备注假设H1。
参数的显著性检验
上面是针对模型的显著性检验作了相关的理论说明，但模型OK(所有的偏回归系数不全为0)，并不代表每一个自变量对因变量都是重要的，即每一个偏回归系数都是OK(所有的偏回归系数都不为0)的，所以，我们还需要对模型的每个偏回归系数进行显著性检验。在检验之前，我们需要先了解一下偏回归系数的期望和方差：
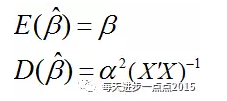
公式推导如下：
既然有了偏回归系数的期望和方差，我们就可以根据标准正态分布来构造t分布了(之所以是t分布，是因为总体方差未知)。如果变量x服从正态分布，则可以通过下面的方式将其转换为标准正态分布：
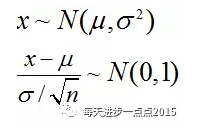
当总体方差未知的时候，则使用样本方差来代替，但要付出一些代价，不再是标准正太分布，而是自由度为n-1的t分布：
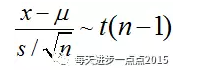
接下来就是要进行参数的显著性检验了，其检验的假设条件为：
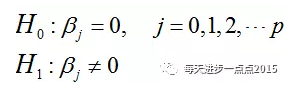
构造检验偏回归系数的t统计量
最终，通过计算统计量t的值与理论的t(n-p-1)值作对比，如果统计量t值大于理论的临界值，则认为可以拒绝原假设H0，否则就得接受原假设。
结语
OK，今天关于线性回归的理论部分，我们就分享到这里，希望对数据挖掘或机器学习比较感兴趣的朋友，能够静下心来好好的整理并推导一遍，以便不时之需（如面试时要求推导）。如果你有任何问题，欢迎在公众号的留言区域表达你的疑问。同时，也欢迎各位朋友继续转发与分享文中的内容，让更多的朋友学习和进步。下一期，我们将运用Python和R语言来实现线性回归模型的落地，期待大家的交流和关注。
关注“每天进步一点点2015”，与小编同进步！
往期从零开始学Python系列：
从零开始学Python【6】--pandas(数据框部分01)
从零开始学Python【7】--pandas(数据框部分02)
从零开始学Python【8】--pandas(数据框部分03)
从零开始学Python【9】--pandas(数据框部分04)
从零开始学Python【10】--matplotlib(条形图)
从零开始学Python【11】--matplotlib(饼图)
从零开始学Python【12】--matplotlib(箱线图)
从零开始学Python【13】--matplotlib(直方图)
从零开始学Python【14】--matplotlib(折线图)
从零开始学Python【15】--matplotlib(散点图)
从零开始学Python【16】--matplotlib(雷达图)
从零开始学Python【17】--matplotlib(面积图)
从零开始学Python【18】--matplotlib(热力图)
从零开始学Python【19】--matplotlib(树地图)