我们知道学习数据挖掘,必须学习矩阵,基本上所有高级一点的算法大都和矩阵有关,然而数学教材里的“矩阵”已经抽象到了很高的程度,没有一定的数学素养,很难理解,因此写这篇博客的目的也是希望可以从事物的本质出发,返璞归真,帮助大家理解矩阵。
之前在网络上看到一篇写“矩阵本质”的博客,写非常好,推荐大家读一读(http://blog.sina.com.cn/s/blog_4bc21c9e010008vz.html),本文打算“也谈矩阵的本质”,分享个人对矩阵的理解。
事实上数学中任何概念的发明都不是无缘无故的,比如有理数、无理数、方差等等,它们大都有现实生活的原型,比如无理数的发现竟是因为希伯索斯发现了正方形的对角线是不可公度(即无法用一个确定数来表示,比如:正方形的边长为1,则对角线的长不是一个有理数),同样“矩阵”的发明也是源于人们不断探索未知的需求,在二维-三维时代,人们觉得可以用一个立体空间来描述所有的对象和事实,然而随着社会的发展,问题复杂的提升,很问题不能仅仅用一两个因素来描述,于是出现了多维空间,最早人们用来描述多维空间的工具是“方程组”,到后来发现“矩阵”有天然的优势来描述多维的世界,于是很自然就被数学家发明出来,发扬光大。
说到这里,其实矩阵的本质已经呼之欲出了,它实际就是用来描述大千世界的万事万物(对象和事实),这个“描述”也可以理解成“映射”,即大千世界的万事万物都可以映射到矩阵中,映射到里面干嘛呢?有时候仅仅为了保存(静态描述),已备后用,有时候是对它进行变换(动态描述),找到它的一些不易被发现的特殊性质,发挥它的作用。
貌似这样解释很玄乎,下面我们就来一步步分解,看看到底是不是真的如此。
一、从坐标系开始
我们先来看看,人们是如何来描述世界的
我们常说珠穆朗玛峰海拔8848米, 是世界第一高峰
我们也说泰山海拔1524米,是五岳之首
我们还说中国的科考潜艇已经可以潜入海底超过了8000米
不然发现,通常我们去描述一个对象(事实)都要基于一个基准(或者说坐标系、参照物)去描述,否则大家的认识就没有统一的标准
如果我说姚明实际只有28cm,你们肯定大嘴巴扇我,但如果我说那是相对于科比来说呢(2.26m-1.98m)
再深奥一点,其实世界是相对的
因此,我们在一个空间中去描述一个对象,首先需要选定基准,简称“基”,一个基称为一维,二个基称为二维,依次类推,N个基称为N维
说到这,你需要意识到一个重要推论:
同一个对象(事实) ,在不同的基准下会有不同的描述
比如,珠穆朗玛峰相对于泰山有7324米高
又比如,同一个人,相机拍摄的角度不一样,照出的来的相片也不一样
很明显,描述不同,但实际都是指向同一个对象
二、什么是矩阵
直观上来看,它是一个按行和列装载了很多数字的容器

它的行与列的数量没有限制,可以是二行的、三列的、….、M行N列
稍微发挥一下我们的想象力:把这里的行或列跟我们空间的中的基准(维)联系到一起
那么我们可以简单定义,当我们选定一组基,就可以用矩阵来描述(或映射)一个对象(事实)
举几个例子帮助大家理解
举例说明1:计算机图形
一个平面上的图形可以在计算机上存储为一些顶点的集合,通过画出顶点,并将顶点用直线相连即可得到图形
如下图的三角形,有三个顶点(0,0)、(1,1)、(1,-1),我们可以用如下矩阵来表示:
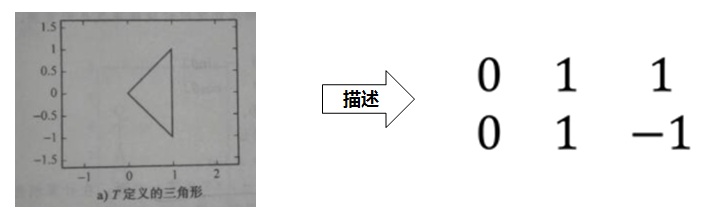
这个例子中,我们默认选了一个二维坐标系(二维基)
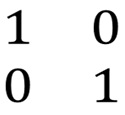
举例说明2:计算机图片

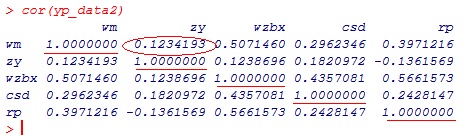
举例说明3:变量与变量相关性
我们知道变量与变量之间相关性可以用相关系数来描述,那么多个变量之间相关性呢?
可以用相关性矩阵来描述,如下
三、矩阵乘法
前面用矩阵描述了一个对象或事实,很明显这个描述是静态的,如何让这个对象或事实“动起来”呢?
矩阵的乘法目的就是这个
不过这里讲的“动”和物理上的运动(路程=速度*时间)是有区别,它是瞬移的,没有过程,也叫“变换”
通俗讲,可以用孙悟空72般变化来帮助理解,高深一点,可以用电子轨道“跃迁”来理解,它们的变化都是瞬间完成的,似乎没有时间
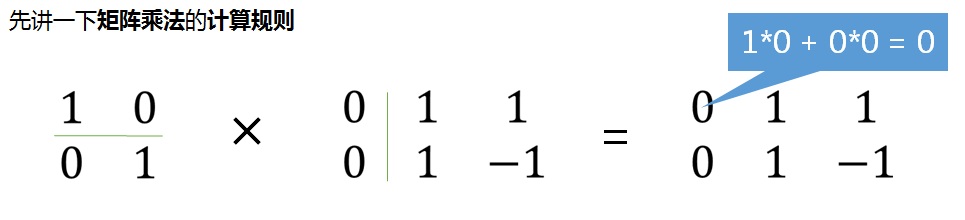
很多人不理解“矩阵乘法”规则为啥这么“复杂”,还不满足“交换定理”
换一种思路来理解上述的计算公式
如果我们把第一个矩阵理解成“基准(坐标系)”,中间那个矩阵理解成矩阵描述的一个对象(前面例子中的三角形),那么第三个矩阵(计算后的矩阵)就可以理解成 第二矩阵在第一个矩阵变换后的结果,换句话如果把第二矩阵放在第一个矩阵(坐标系)下,那么它的样子会变成第三个矩阵
这样也就解释了为啥矩阵乘法不能满足“交换定理”
接下来,我们从矩阵的“三种”经典变换来加深一下上述概念的理解

小结一下:
通过前面的内容,我们发现所谓“变换”实质就是由于坐标系的变化引起的
而我们前面也讲过,同一个对象或事实,在不同的基准(坐标系)下有不同的描述
这个“不同的描述”就是“变换”引起的结果
如果我们想知道当前坐标系下的一个描述,在另一个坐标系下会是如何的(长什么样子),只要对它实施“矩阵乘法”即可
四、矩阵的相似性
在前面的讨论中,我们知道同一个对象或事实,在不同的基准(坐标系)下有不同的描述,而矩阵是用来描述对象或事实的
那现在就会碰到这样的问题:
如果给你两个矩阵,你怎么才能知道它们是不是描述同一个对象或事实呢?
比如下面两张图片,存在计算里面,肯定是两个不同的矩阵,但它实际是一个人

为此,数学家们绞尽脑汁,终于想出了一个矩阵相似性定理,如下定义:

有了这个定理,就不怕认不出自家兄弟了
五、矩阵的对角化
在前面的讨论中,我们知道同一个对象或事实,在不同的基准(坐标系)下有不同的描述
但是你们有没有想过:描述也有“好坏”之分啊
比如,从不同角度(坐标系)拍出来的相片,也有“美丑”之分

那矩阵如何来区分“美丑”呢?
对于数学家来说,一个矩阵除了对角线上的数字不是0,其他都是0的矩阵是最美的,这种矩阵我们称为“对角化”矩阵
原因是这种“对角化”矩阵有很多优良的数学计算特性,比如幂乘

六 矩阵的特征值与特征向量
现在请大家抛开前面讲的内容,回到对象或事实的本质上来
任何对象或事实都是有特征的对吗?
假如没有特征,你怎么去描述一个对象或事实?
既然矩阵是对象或事实的描述,那么矩阵一定也有特征
在一个空间中,我们是怎么去描述特征的呢?
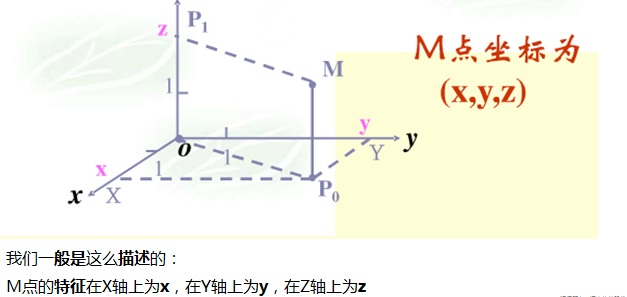
我们回过头在去看看“对角化矩阵”
它只有对角线上的数据不为0
我们把每一行或列,看成一个基,对角线上的数字,正好对应于对象或事实在该基上的特征
因此,矩阵对角化实质就是矩阵寻找特征值的过程
特征值的大小能反映该特征的重要程度
以上就是本篇博客的主要内容,从矩阵的本质出发,解释了矩阵学习中常见的几个概念:矩阵乘法、相似性、对角化以及特征值与特征向量,
由于个人理解有限,有不严谨的地方欢迎指正。