文章发布于公号【数智物语】 （ID：decision_engine），关注公号不错过每一篇干货。
来源 | SAMshare（id:SAMshare）
作者 | samshare
"本次主要讲解的内容就是特征降维，主要涉及PCA以及一些常见分析方法。"
01Index
一，PCA降维算法
1. 内积与投影
2. 基与基变换
3. 方差
4. 协方差
5. 协方差矩阵
6. 协方差矩阵对角化
7. PCA算法步骤
8. PCA实例
9. PCA的Python操作
二，LDA降维算法
1. LDA介绍
2. LDA的优缺点
3. LDA的Python操作
在机器学习中，我们有的时候会遇到维度灾难，当模型的训练入参有很多的时候，往往是需要很多的时间和资源去训练的，而这不是我们想要看到的结果。一般情况下，我们都是会对源数据进行特征处理，提取对预测更加有效的特征。
有的时候，我们会得到比较高维的特征向量，而这里面往往包含很多的噪声与冗余数据，所以我们需要通过降维的方式去获取特征更加有效的信息，一来提高特征表达能力，二来提高模型训练的效率。
02PCA降维算法
PCA（Principal Components Analysis），即主成分分析，是降维操作中最经典的方法，它是一种线性的、无监督、全局性的降维算法，旨在找到数据中的"主要成分"，提取主成分从而达到降维的目的。PCA是一种无监督算法，也就是我们不需要标签也能对数据做降维，这就使得其应用范围更加广泛了，但是PCA也有一个问题，原来的数据中比如包括了年龄，性别，身高等指标降维后的数据既然维度变小了，那么每一维都是什么含义呢？这个就很难解释了，所以PCA本质来说是无法解释降维后的数据的物理含义。
在了解PCA之前，有一些基础的名词需要温习一下：
01内积与投影
内积运算将两个向量映射为一个实数，下面是两个维数相同的向量的内积：
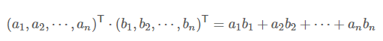
假设存在两个点A,B，其在坐标轴的位置如下图：
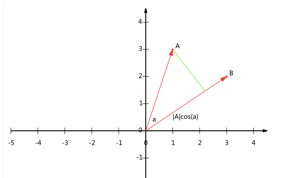
我们从A向B引一条垂线，也就是A在B上的投影，其夹角为a，则投影的矢量长度为|A|cos(a)，其中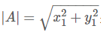
是向量A的模，也就是A线段的标量长度。
而内积的另一种表现形式为：
也就是说，当B的模为1的时候，也就是单位向量的时候，内积可以表示为：
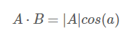
也就是A与B的内积值等于A向B所在直线投影的矢量长度。
02基与基变换
基可以理解为单位向量，基都是正交的（即内积为0，直观来说就是相互垂直），并且是线性无关的。
基变换指的是当前向量和一个基进行内积运算，得到的结果作为新的坐标分量。
假设存在一个点（3,2），一般我们都会取(1,0)和(0,1)为基，也就是我们的X和Y轴方向。如果我们取(1,1)和(-1,1)为我们的基，但我们希望基的模为1，这样子会方便计算，所以可以除以当前的模长，所以上面的基就变成了：
如下图所示：
所以，进行基变换，只需要进行一次内积运算：
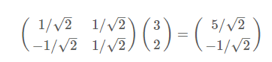
03方差
一个字段的方差可以看做是每个元素与字段均值的差的平方和的均值，即：
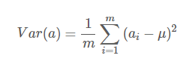
一般我们都会把均值为化为0，即进行一次变换，所以方差可以表示为：
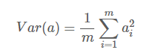
04协方差
如果单纯地选择方差最大的方向，则无法保证两个字段之间相互独立，因为我们需要的是尽可能多地保留原始信息，但又是相互独立，这里我们引入一下概念，协方差，用来表示两个字段的相关性，公式为：
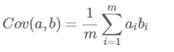
协方差：度量各个维度偏离其均值的程度。协方差的值如果为正值，则说明两者是正相关的(从协方差可以引出“相关系数”的定义)，结果为负值就说明负相关的，如果为0，也是就是统计上说的“相互独立”。
所以，我们的目标就是让两个字段的协方差为0，为了协方差为0，选择第二个基的时候，必须要在第一个基的正交方向上选择。
我们说的PCA降维，就是把N维的特征，降到K维（0 < K < N），也就是说要选择k个单位正交基，并且尽可能让方差最大化。
05协方差矩阵
在统计学与概率论中，协方差矩阵的每个元素是各个向量元素之间的协方差，是从标量随机变量到高维度随机向量的自然推广。
假设存在矩阵X：
其协方差矩阵为：
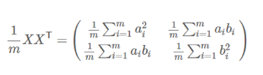
可以看出，协方差矩阵的对角线元素为两个字段的方差，而其他元素为矩阵的协方差，按照我们之前的说法，我们需要得到协方差为0，并且方差最大的转换。
06协方差矩阵对角化
根据上述推导，我们发现要达到优化目前，等价于将协方差矩阵对角化：即除对角线外的其它元素化为0，并且在对角线上将元素按大小从上到下排列，这样我们就达到了优化目的。这样说可能还不是很明晰，我们进一步看下原矩阵与基变换后矩阵协方差矩阵的关系。
设原始数据矩阵X对应的协方差矩阵为C，而P是一组基按行组成的矩阵，设Y=PX，则Y为X对P做基变换后的数据。设Y的协方差矩阵为D，我们推导一下D与C的关系：
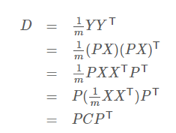
我们要找的P不是别的，而是能让原始协方差矩阵对角化的P。换句话说，优化目标变成了寻找一个矩阵P，满足PCP^T是一个对角矩阵，并且对角元素按从大到小依次排列，那么P的前K行就是要寻找的基，用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。
07PCA算法步骤
设有mXn维数据。
1）将原始数据按列组成n行m列矩阵X
2）将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值
3）求出协方差矩阵C=1mXXT
4）求出协方差矩阵的特征值及对应的特征向量
5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P
6）Y=PX即为降维到k维后的数据
08PCA实例
假设存在2维数据
：,需要将其降至1维。
1）均值归0：目前每个维度的均值均为0，无需变换。
2）求协方差矩阵
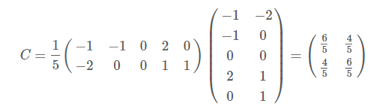
3）求解特征值以及特征向量
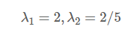
可以参考：https://jingyan.baidu.com/article/27fa7326afb4c146f8271ff3.html
4）标准化特征向量
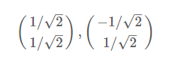
5）得到对角矩阵P并验证对角化
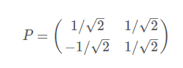
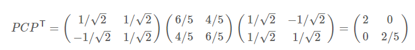
6）因为需要得到1维矩阵，因此用P的第一行乘以原矩阵即可：
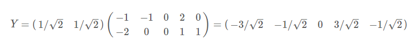
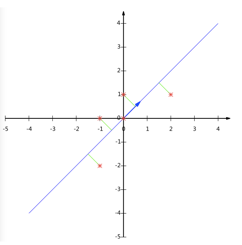
降维投影如下图所示：
09Python操作
# 使用sklearn进行PCA降维
import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1,2,66,-1], [-2,6,58,-1], [-3,8,45,-2], [1,9,36,1], [2,10,62,1], [3,5,83,2]]) #导入数据，维度为4
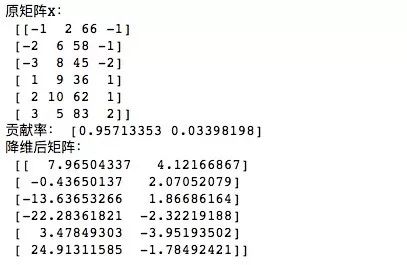
print('原矩阵X：\n', X)
pca = PCA(n_components=2) #降到2维
pca.fit(X) #训练
newX=pca.fit_transform(X) #降维后的数据
print('贡献率：', pca.explained_variance_ratio_)
print('降维后矩阵：\n', newX)
'''
参数解释：
n_components: 我们可以利用此参数设置想要的特征维度数目，可以是int型的数字，也可以是阈值百分比，如95%，让PCA类根据样本特征方差来降到合适的维数，也可以指定为string类型，MLE。
copy：bool类型，TRUE或者FALSE，是否将原始数据复制一份，这样运行后原始数据值不会改变，默认为TRUE。
whiten：bool类型，是否进行白化（就是对降维后的数据进行归一化，使方差为1），默认为FALSE。如果需要后续处理可以改为TRUE。
explained_variance_： 代表降为后各主成分的方差值，方差值越大，表明越重要。
explained_variance_ratio_： 代表各主成分的贡献率。
inverse_transform()： 将降维后的数据转换成原始数据，X=pca.inverse_transform(newX)。
'''
output：
03LDA降维算法
线性判别分析（Linear Discriminant Analysis，LDA）是一种有监督学习算法，也是经常被拿来降维，它和PCA的区别在于是否存在标签，其中心思想就是—— 最大化类间距离和最小化类内距离。
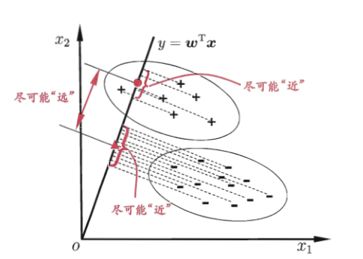
而PCA的不足在于不能很好地分开不同类别的数据，如下图：
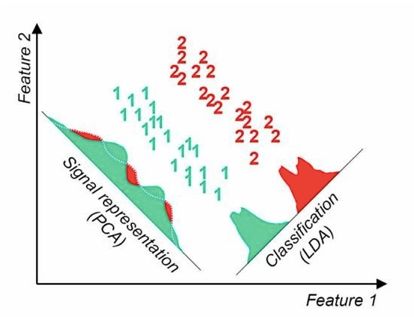
LDA算法既可以用来降维，又可以用来分类，但是目前来说，主要还是用于降维。在我们进行图像识别图像识别相关的数据分析时，LDA是一个有力的工具。下面总结下LDA算法的优缺点：
01优点：
1）在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。
2）LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。
02缺点：
1）LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。
2）LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
3）LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。
4）LDA可能过度拟合数据。
03Python操作
import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
y = np.array([1, 1, 1, 2, 2, 2])
clf = LinearDiscriminantAnalysis()
clf.fit(X, y)
LinearDiscriminantAnalysis(n_components=None, priors=None, shrinkage=None,
solver='svd', store_covariance=False, tol=0.0001)
print(clf.predict([[-0.8, -1]]))04Reference
1）Reference十分钟搞定PCA主成分分析
https://blog.csdn.net/tangyudi/article/details/80188302#comments
2）PCA的数学原理
http://blog.codinglabs.org/articles/pca-tutorial.html
星标我，每天多一点智慧
