正态分布是我们经常听到的一个名词,又叫高斯分布,许多模型或算法都要求数据服从正态分布,比如:pearson相关系数、线性回归等。样子如下:
plot(density(rnorm(1000000))) # R语言代码
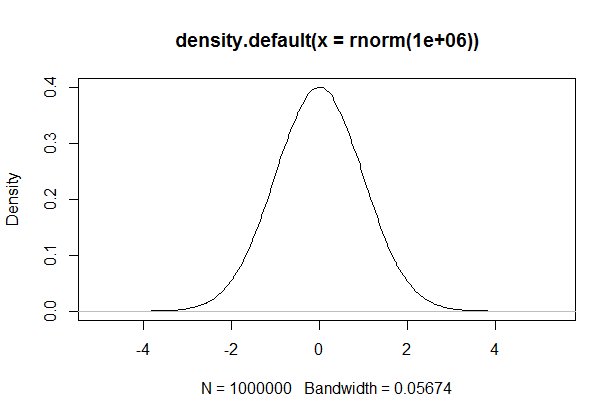
关于正态分布的详细介绍可以参照 百度百科 维基百科,本文简单介绍一下正态分布在Excel、R和Python中的检验。
1. 正态分布在Excel中的检验
我在Excel中并没有发现有检验正态分布的函数(但是有一些正态分布相关的函数),所以我们不能直接使用一个函数来检验一列数据是否服从正态分布。
那怎么判断一列数据是否服从正态分布呢?我认为可以从正态分布的特征(均值=中位数=众数,偏度=0,峰度=0)来主观判断。
上面提到的几个指标,Excel可以使用数据分析功能非常方便的输出出来,如下:
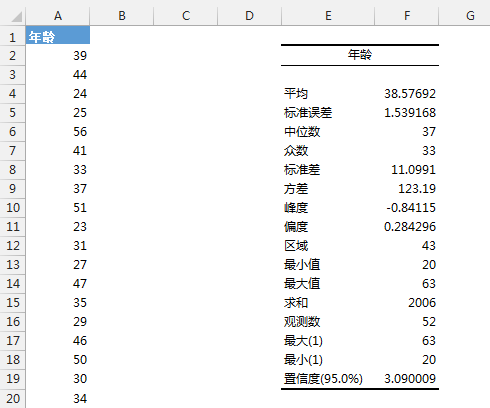
输出方法:数据选项卡→数据分析→选择描述统计功能。
若没有数据分析功能,需要在Excel选项中加载出来:文件→选项→加载项→Excel加载项 转到→勾选分析工具库。
可以看到A列(一个52条记录的年龄数据)的描述统计(E、F列)。可以看到均值≈中位数(众数表示出现频率最高的数值,不是非常异常可以不用考虑),偏度和峰度都很小,接近0;所以我们可以主观判断年龄数据服从正态分布。
PS:非严格条件下,统计学中认为样本量≥30的样本可以认为其服从正态分布。
2. 正态分布在R中的检验
使用专业的统计软件,一般我们会做QQ图来直观的看数据的正态分布情况,当然也会有许多检验函数来做正态分布的假设检验。
我们来做QQ图:
qqnorm(df$Age, main='Normal Q-Q Plot')
qqline(df$Age)
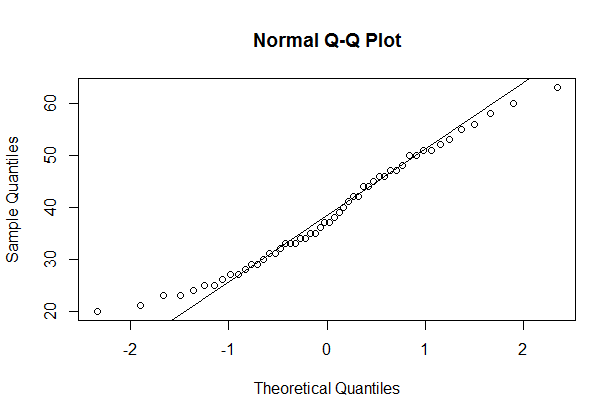
可以看到散点几乎都分布在直线上,基本可以判断为服从正态分布。
我们来做正态分布检验(使用:Shapiro-Wilk normality test):
shapiro.test(df$Age)

可以看到P=0.2187>0.05,接受服从正态分布的原假设(严格的说法是不能在α=0.05的显著性水平下拒绝原假设)。
3. 正态分布在Python中的检验
我们按照同样的步骤(画图直观看、QQ图、假设检验)来看一下这三步操作在Python中的实现。
来看一下Age的直方图:
%matplotlib inline
import seaborn as sns
from scipy import stats
sns.distplot(df.Age, kde=True, fit=stats.norm)
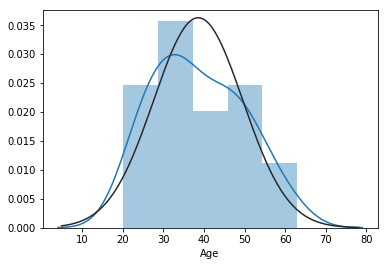
可以看到直方图呈中间高两边低的分布,概率密度曲线也与比较接近正态分布曲线。
QQ图:
import statsmodels.api as sm
qqplot = sm.qqplot(df.Age, fit=True, line='45')
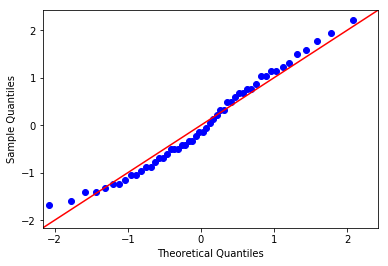
同样地,散点几乎都分布在了斜线上。
正态分布检验:
stats.normaltest(df.Age)
输出内容:NormaltestResult(statistic=4.1118734600586535, pvalue=0.12797290335273284)
可以看到P值>0.05,接受服从正态分布的原假设。
细心的朋友会发现R和Python的检验结论虽然一致,但是得到的参数并不相同。
我认为关于正态分布的检验还要看具体场景,并不是一定要非常严格的限定α=0.05,可以适当的进行调整,当数据量大的时候甚至可以直接默认数据服从正态分布,或者采用不要求正态分布的算法。
以上,如有不妥之处还请多多指正,数据文件及代码请查阅附件。