一元（多元）线性回归分析之R语言实现

上篇介绍了《一元（多元）线性回归分析之Excel实现》，本篇来探讨一下回归分析在R语言中的实现，我们将从更专业的角度对模型进行一些解读。

1. 一元线性回归

同样，我们仍然使用R中自带的women数据集，来看一下数据样式：

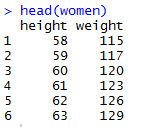
1.1 数据探索

首先做散点图查看数据的分布情况：

plot(women$height, women$weight,

     xlab = "Height (in inchs)", ylab = "Weight (in pounds)")

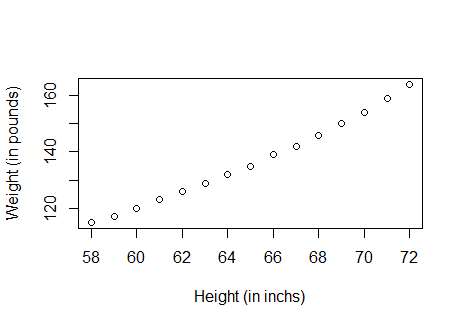
可以看到散点分布呈现线性规律，说明适合构建线性回归方程。

1.2 构建模型

fit <- lm(weight ~ height, data = women)

可以看到R做线性回归非常简单，只需要简单的lm函数即可。

1.3 模型解读

# 查看模型

summary(fit)

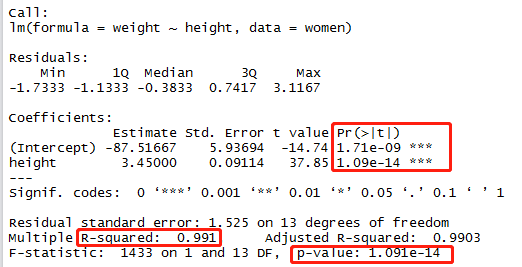
首先看R-squared:  0.991，说明模型的解释性非常好，能够解释99%的方差，且F检验的p-value: 1.091e-14远远小于0.05，说明模型通过了F检验；

再看截距项和系数，都通过了t检验，且height的系数为正，表明随着身高的增长，体重也增长，符合客观事实。

得到回归方程：weight = -87.51667 + 3.45000*height

查看一下模型拟合效果：

plot(women$height, women$weight,

     xlab = "Height (in inchs)", ylab = "Weight (in pounds)")

abline(fit)

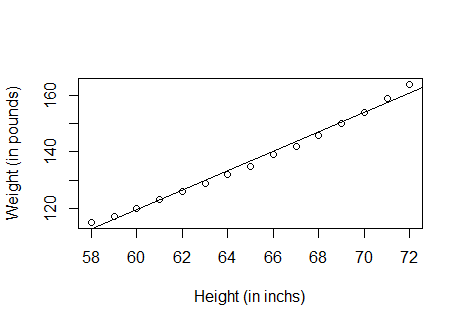
回归诊断：

par(mfrow=c(2,2)) # 设置一个画布上输出2*2个图形

plot(fit)

par(mfrow=c(1,1)) # 恢复设置

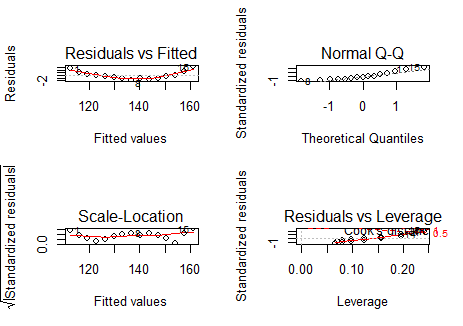
上图缩放后可能不够清晰，我们来解读一下：

左上图：残差与拟合图，理论上散点应该散乱的分布在横线两侧，但是此图明显有一个曲线关系，说明我们的模型需要加入一个二次项（这一点从散点图亦可以看出来）。

右上图：正太Q-Q图，用于检验因变量的正太分布性，若服从正太分布，则散点应分布在一条直线上，此图满足表明满足正态性假设。

左下图：齐方差检验，若满足其方差，则散点在水平线周围随机分布，此图满足齐方差检验。

右下图：独立性检验，即一个样本是否会影响另一个样本，我们的样本数据似乎并不存在这样的问题。

1.4 模型修正

增加一个二次项进模型：

fit2 <- lm(weight ~ height + I(height^2), data = women)

summary(fit2)

plot(women$height, women$weight,

     xlab = "Height (in inchs)", ylab = "Weight (in pounds)")

lines(women$height, fitted(fit2))

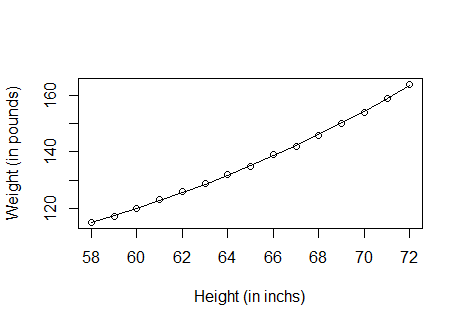
得到R-squared:  0.9995，模型效果得到了提升；拟合效果也有一些改善。

2. 多元线性回归

相较于一元，多元线性回归需要考虑的问题较多，我们还是用salary数据集（数据文件见上篇）。

# 导入数据

dataset <- read.csv("C:\\Users\\huzhanpeng\\Desktop\\Regression\\salary.csv")

df <- dataset[, -1]

head(df)

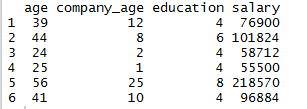
2.1 数据探索

做散点图矩阵，查看各变量之间的关系

library(car)

scatterplotMatrix(df, spread = F, smoother=loessLine, main = "Scatter Plot Matrix")

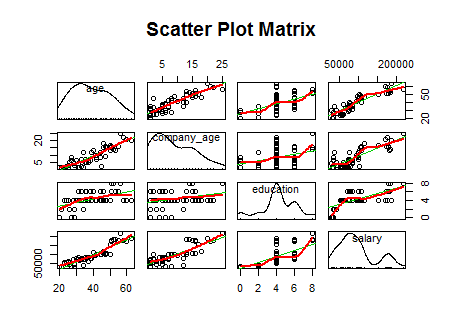
可以看到salary与其余三个变量都有比较明显的正的线性相关关系，另外age和company_age也有明显的正相关。

我们来看一下各变量间的相关系数：

cor(df)

2.2 构建模型

fit <- lm(salary ~ .,data = df) # 用.表示数据框中的其余变量

2.3 模型解读

summary(fit)

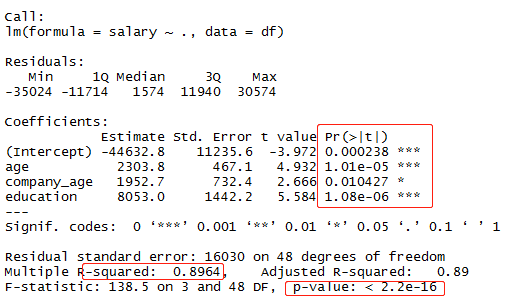
可以看出模型效果显著，且通过了F检验，截距项和系数也都通过了t检验。

2.4 模型检验

我们对方程进行进一步检验，以检查回归方程是否满足模型的先验条件及模型的稳健性。

2.4.1 正态性、独立性、线性、齐方差（使用car包）

# 正态性

qqPlot(fit, labels = rownames(df), id.method = 'identify',

       simulate = TRUE, main = "Q-Q Plot")

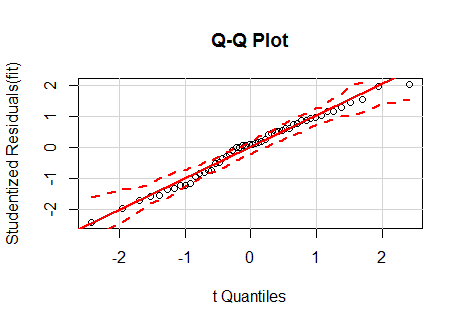
可以看到散点都分布在直线两侧，且没有明显偏离虚线区间的点，说明方程满足正态性的先验条件。

# 独立性

p值0.636接受原假设，说明无自相关性，误差项之间独立。

# 线性

crPlots(fit)

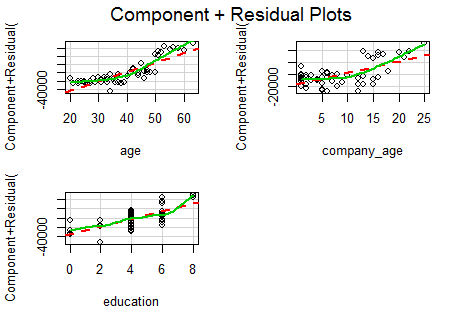
可以看到满足此条件

# 齐方差

p>0.05,接受原假设，误差方差不变

2.4.2 多重共线性

library(car)

vif(fit)

# 一般sqrt(vif)>2就表明存在多重共线性的问题

sqrt(vif(fit)) > 2

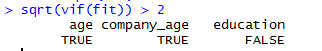
可以看出：age和company_age都引入方程时，方程存在多重共线性（两者的相关系数为0.87，上面已得知）。

如果仅仅是做预测，那么多重共线性并不构成问题。但是如果还要对每个预测变量进行解释，那么就必须解决这个问题。最常见的方法就是删除某个存在多重共线性的变量。另外一个可用的方法便是岭回归，专门用来处理多重共线性的问题。

2.4.3 异常值

异常值检验主要是从模型的稳健性考虑，是否有离群点、强影响点、高杠杆值的影响。

library(car)

influencePlot(fit, id.method = "identify", main = "Influence Plot", 

    sub = "Circle size is proportial to Cook's Distance")

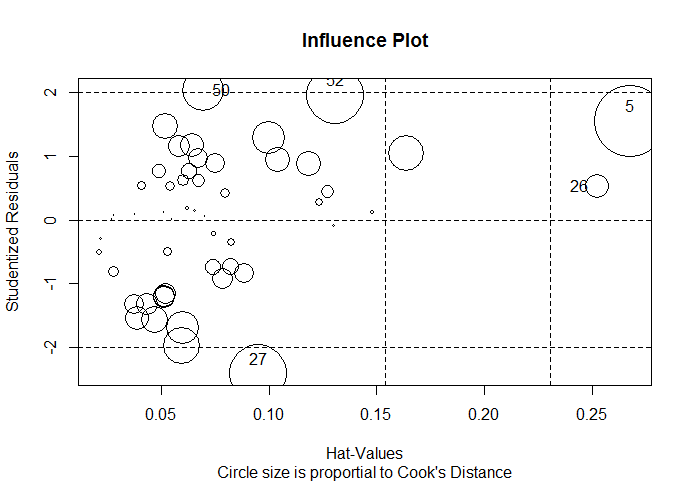
# 纵坐标超过+2或小于-2的散点可被认为是离群点

# 水平轴超过0.2或0.3的散点有高杠杆值

# 圆圈大小与影响成比例，圆圈很大的点可能是对模型参数的估计造成的不成比例影响的强影响点

2.5 模型评估

2.5.1 K重交叉验证

在k 重交叉验证中，样本被分为k个子样本，轮流将k1个子样本组合作为训练集，另外1个子样本作为保留集。这样会获得k 个预测方程，记录k 个保留样本的预测表现结果，然后求其平均值。 [当n 是观测总数目， k 为n 时，该方法又称作刀切法（jackknifing）。 ]

bootstrap 包 中 的 crossval() 函 数 可 以 实 现 k 重 交 叉 验 证 。

# Function for k-fold cross-validated R-square

shrinkage <- function(fit, k = 10) {

    require(bootstrap)

    # define functions

    theta.fit <- function(x, y) {

        lsfit(x, y)

    }

    theta.predict <- function(fit, x) {

        cbind(1, x) %*% fit$coef

    }

    

    # matrix of predictors

    x <- fit$model[, 2:ncol(fit$model)]

    # vector of predicted values

    y <- fit$model[, 1]

    

    results <- crossval(x, y, theta.fit, theta.predict, ngroup = k)

    r2 <- cor(y, fit$fitted.values)^2

    r2cv <- cor(y, results$cv.fit)^2

    cat("Original R-square =", r2, "\n")

    cat(k, "Fold Cross-Validated R-square =", r2cv, "\n")

    cat("Change =", r2 - r2cv, "\n")

}



shrinkage(fit)

模型的R²从0.896降到了0.876，变化不大。

2.5.2 变量的重要性

进入方程的几个变量谁起到的作用更大呢？

方法1：

zdf <- as.data.frame(scale(df))

zfit <- lm(salary ~ ., data = zdf)

coef(zfit)

可以看到三个变量之间的重要性差别不是非常明显，age最重要

方法2：

# 相对权重（relative weight）方法

relweights <- function(fit, ...) {

  R <- cor(fit$model)

  nvar <- ncol(R)

  rxx <- R[2:nvar, 2:nvar]

  rxy <- R[2:nvar, 1]

  svd <- eigen(rxx)

  evec <- svd$vectors

  ev <- svd$values

  delta <- diag(sqrt(ev))

  

  # correlations between original predictors and new orthogonal variables

  lambda <- evec %*% delta %*% t(evec)

  lambdasq <- lambda^2

  

  # regression coefficients of Y on orthogonal variables

  beta <- solve(lambda) %*% rxy

  rsquare <- colSums(beta^2)

  rawwgt <- lambdasq %*% beta^2

  import <- (rawwgt/rsquare) * 100

  lbls <- names(fit$model[2:nvar])

  rownames(import) <- lbls

  colnames(import) <- "Weights"

  

  # plot results

  barplot(t(import), names.arg = lbls, ylab = "% of R-Square", 

          xlab = "Predictor Variables", main = "Relative Importance of Predictor Variables", 

          sub = paste("R-Square = ", round(rsquare, digits = 3)), 

          ...)

  return(import)

}



# using relweights()

relweights(fit, col = "lightgrey")

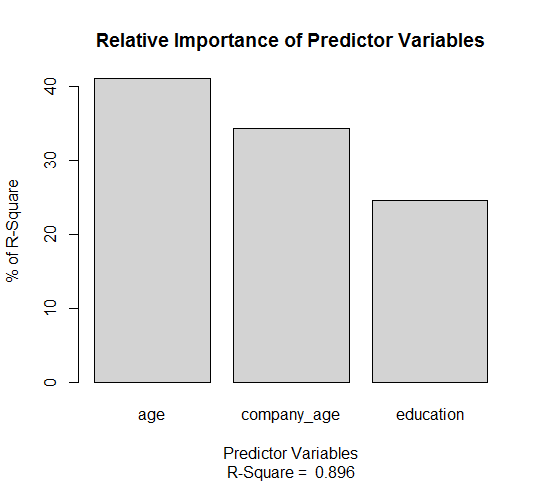
可以得出同样的结论：age这个变量较company_age和education对回归方程的影响更大。

2.6 模型修正

由于存在多重共线性的问题，我们对模型进行修正处理（如前文所述，若为预测用，可以不用考虑共线性问题）。

2.6.1 剔除引起共线性的变量

根据前文，我们知道了age和company_age存在高度相关，且age对模型更重要，所以我们剔除company_age这个变量

fit2 <- lm(salary ~ age + education, data=df)

summary(fit2)

可以看到：剔除了company_age后模型效果依然不错，R²从0.896变为了现在的0.881，变化不大，效果很好；方程也通过了F检验、t检验。

2.6.2 岭回归

require(ridge)

fit.ridge<-linearRidge(salary ~ ., data=df)

summary(fit.ridge)

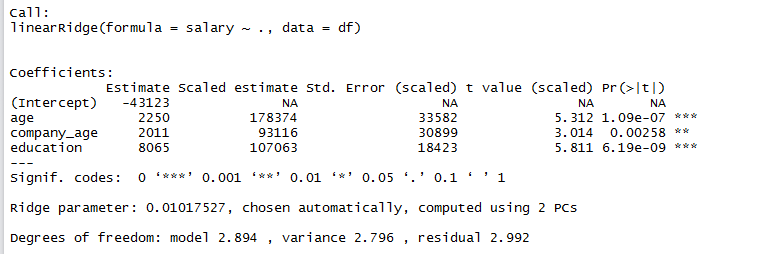
对于多元线性回归，当自变量较多时，可以先使用逐步回归的方法来筛选变量进入模型，R实现起来非常简单，不再赘述。

以上，不正之处还请大家指出，如有更好的建议也请不吝赐教，也欢迎大家多多推荐，谢谢。