作者：张磊 从事AI医疗算法相关工作
个人微信公众号：
机器学习算法那些事（微信ID：zl13751026985）
目录
1. KNN算法原理
2. KNN算法三要素
3. KNN算法之暴力实现原理
4. KNN算法之KD树实现原理
5. KNN算法之训练样本不平衡情况
6. 算法优缺点
1. KNN算法原理
KNN算法是选择与输入样本在特征空间内最近邻的k个训练样本并根据一定的决策规则，给出输出结果 。
决策规则：
分类任务：输出结果为k个训练样本中占大多数的类 。
回归任务：输出结果为k个训练样本值的平均值 。
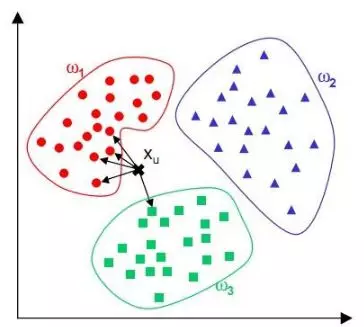
如下图的分类任务，输出结果为w1类 。
2. KNN算法三要素
K值的选择、距离度量和分类决策规则是K近邻算法的三个基本要素。当三个要素确定后，对于任何一个新的输入实例，它所属的Y值也确定了，本节介绍了三要素的含义。
1. 分类决策规则
KNN算法一般是用多数表决方法，即由输入实例的K个邻近的多数类决定输入实例的类。这种思想也是经验风险最小化的结果。
训练样本为(xi , yi)。当输入实例为 x，标记为c，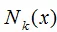
是输入实例x的k近邻训练样本集。
我们定义训练误差率是K近邻训练样本标记与输入标记不一致的比例，误差率表示为：
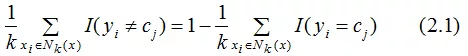
因此，要使误差率最小化即经验风险最小，就要使(2.1)式右端的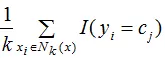
最大，即K近邻的标记值尽可能的与输入标记一致，所以多数表决规则等价于经验风险最小化。
2. K值的选择：
K取值较小时，模型复杂度高，训练误差会减小，泛化能力减弱；K取值较大时，模型复杂度低，训练误差会增大，泛化能力有一定的提高。
KNN模型的复杂度可以通过对噪声的容忍度来理解，若模型对噪声很敏感，则模型的复杂度高；反之，模型的复杂度低。为了更好理解模型复杂度的含义，我们取一个极端，分析K=1和K="样本数"的模型复杂度。
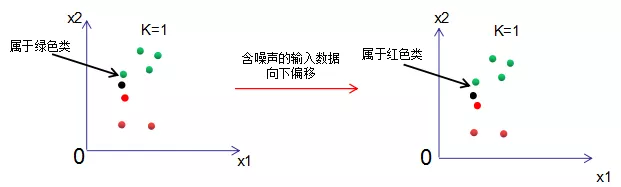
由上图可知，K=1时，模型输出的结果受噪声的影响很大。
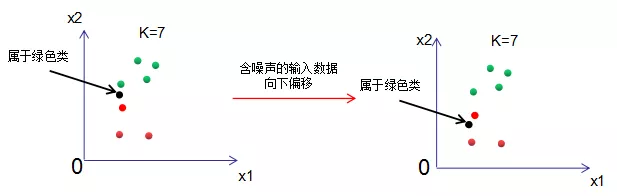
由上图可知，样本数等于7，当K=7时，不管输入数据的噪声有多大，输出结果都是绿色类，模型对噪声极不敏感，但是模型太过简单，包含的信息太少，也是不可取的。
通过上面两种极端的K选取结果可知，K值选择应适中，K值一般小于20，建议采用交叉验证的方法选取合适的K值。
3. 距离度量
KNN算法用距离来度量两个样本间的相似度，常用的距离表示方法：
(1)、欧式距离
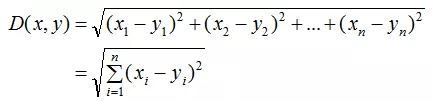
(2)、曼哈顿距离
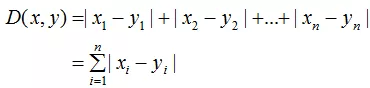
(3)、闵可夫斯基距离
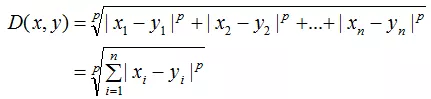
可以看出，欧式距离是闵可夫斯基距离在p=2时的特例，而曼哈顿距离是p=1时的特例 。
3. KNN算法之暴力实现方法
暴力搜索（brute-force search）是线性扫描输入实例与每一个训练实例的距离并选择前k个最近邻的样本来多数表决，算法简单，但是当训练集或特征维度很大时，计算非常耗时，故这种暴力实现原理是不可行的 。
4. KNN算法之kd树实现方法
kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构，构造kd树相当于不断用垂直于坐标轴的超平面将k维空间进行划分，构成一系列的K维超矩形区域，kd树省去了对大部分数据的搜索，大大的较少了计算量。
kd树的KNN算法实现包括三部分：kd树的构建，kd树的搜索和kd树的分类。
1. 构建kd树
kd树实质是二叉树，其划分思想与cart树一致，即切分使样本复杂度降低最多的特征。kd树认为特征方差越大，则该特征的复杂度亦越大，优先对该特征进行切分 ，切分点是所有实例在该特征的中位数。重复该切分步骤，直到切分后无样本则终止切分，终止时的样本为叶节点。
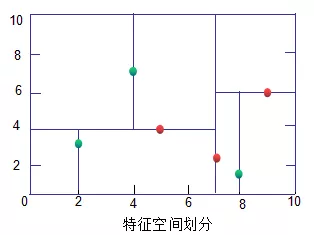
【例】给定一个二维空间的数据集：
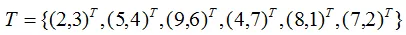
构造kd树的步骤：
(1)、数据集在维度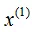
和
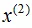的方差分别为6.9和5.3，因此首先从
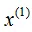维度进行切分。
(2)、 数据集在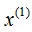
维度的中位数是7，以平面
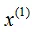=7将空间分为左右两个矩形。
(3)、分别对左右两个矩形的样本在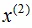
维度的中位数进行切分。
(4)、重复步骤（2）（3），直到无样本，该节点为叶子节点。
如下图，绿色为叶子节点 ，红色为节点和根节点。
2. KD树搜索
(1)、搜索路径从根节点到叶节点，在KD树里面找到包含目标点的叶子节点。
(2)、搜索路径从叶节点到根节点，找到距离目标点最近的样本实例点。过程不再复述，具体方法请参考李航博士《统计学习方法》。
3. KD树预测
每一次搜寻与输入样本最近的样本节点，然后忽略该节点，重复同样步骤K次，找到与输入样本最近邻的K个样本 ，投票法确定输出结果。
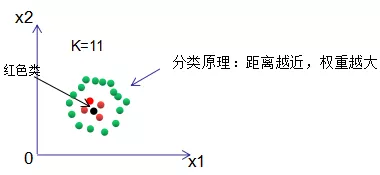
5. KNN算法之训练样本不平衡情况
若正负样本处于不平衡状态，运用投票决策的KNN算法判断输入样本的所属类别：
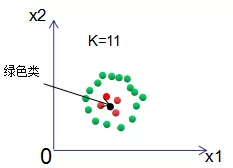
结果显示输入样本为绿色类 。原因是红色类的个数远远小于绿色样本，导致出现的分类错误 。
（1）若分类决策选择限定半径最近邻法，即以输入样本为圆心，最大半径R的圆内选择出现次数最多的类做为输入样本的类 。如下图，黑色样本的分类结果正确。
（2）投票法是默认每个样本的权重相等，我们假定权重与距离成反比，即距离越大，对结果的影响越小，那么该样本的权重也越小，反之，权重则越大，根据权重对输入样本进行分类 。这种思想与adaBoost算法相似，分类性能好的弱分类器给予一个大的权重 。
分类过程：
(1)、选择与输入样本距离X0最近的K个训练样本Xi（i = 1,2,...,K），d(X0,Xi)表示输入样本和训练样本的距离。
(2)、根据距离与样本成反比的性质将距离转化成权重Wi，Wi表示输入样本X0与训练样本Xi的权重。
(3)、我们累加每一类的样本权重，并认为该权重占所有权重和的比例是该类的生成概率，概率最大的类就是输入样本的分类结果。
假设目标是二分类{C1，C2}，表达式：
若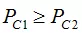
，则分类结果为C1类，反之C2类。
回归过程：
（1）（2）步骤与分类过程一直，第（3）步使用如下表达式得到回归值：
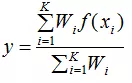
其中，y为输出结果，f(xi)为最近邻样本的值。若权重相同的话，则输出结果为K个训练样本的平均值。
用权重思想重新对上例进行分类，可得输入样本为红色类。
6. KNN算法优缺点
优点：
1）算法简单，理论成熟，可用于分类和回归。
2）对异常值不敏感。
3）可用于非线性分类。
4）比较适用于容量较大的训练数据，容量较小的训练数据则很容易出现误分类情况。
5）KNN算法原理是根据邻域的K个样本来确定输出类别，因此对于不同类的样本集有交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为合适。
缺点：
1）时间复杂度和空间复杂度高。
2）训练样本不平衡，对稀有类别的预测准确率低。
3）相比决策树模型，KNN模型可解释性不强。
参考：
https://www.cnblogs.com/pinard/p/6061661.html
推荐阅读：
公众号后台回复关键词学习
回复 免费 获取免费课程
回复 直播 获取系列直播课
回复 Python 1小时破冰入门Python
回复 人工智能 从零入门人工智能
回复 深度学习 手把手教你用Python深度学习
回复 机器学习 小白学数据挖掘与机器学习
回复 贝叶斯算法 贝叶斯与新闻分类实战
回复 数据分析师 数据分析师八大能力培养
回复 自然语言处理 自然语言处理之AI深度学习
