作者简介：
Treant 人工智能爱好者社区专栏作者
引言
PageRank是Sergey Brin与Larry Page于1998年在WWW7会议上提出来的，用来解决链接分析中网页排名的问题。在衡量一个网页的排名，直觉告诉我们：
当一个网页被更多网页所链接时，其排名会越靠前；
排名高的网页应具有更大的表决权，即当一个网页被排名高的网页所链接时，其重要性也应对应提高。
对于这两个直觉，PageRank算法所建立的模型非常简单：一个网页的排名等于所有链接到该网页的网页的加权排名之和：
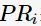表示i个网页的PageRank值，用以衡量每一个网页的排名；若排名越高，则其PageRank值越大。网页之间的链接关系可以表示成一个有向图
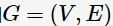，边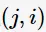
代表了网页j链接到了网页i；
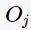为网页j的出度，也可看作网页j的外链数（ the number of out-links）。
假定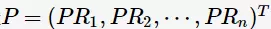
为n维PageRank值向量，A为有向图G所对应的转移矩阵，
n个等式（1）改写为矩阵相乘：
但是，为了获得某个网页的排名，而需要知道其他网页的排名，这不就等同于“是先有鸡还是先有蛋”的问题了么？幸运的是，PageRank采用power iteration方法破解了这个问题怪圈。欲知详情，请看下节分解。
求解
为了对上述及以下求解过程有个直观的了解，我们先来看一个例子，网页链接关系图如下图所示：
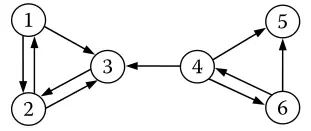
那么，矩阵A即为
所谓power iteration，是指先给定一个P的初始值
，然后通过多轮迭代求解:
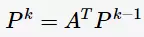
最后收敛于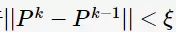
，即差别小于某个阈值。我们发现式子（2）为一个特征方程（characteristic equation），并且解P是当特征值（eigenvalue）为1时的特征向量（eigenvector）。为了满足（2）是有解的，则矩阵AA应满足如下三个性质：
stochastic matrix，则行至少存在一个非零值，即必须存在一个外链接（没有外链接的网页被称为dangling pages）；
不可约（irreducible），即矩阵A所对应的有向图G必须是强连通的，对于任意两个节点u,v∈V，存在一个从u到v的路径；
非周期性（aperiodic），即每个节点存在自回路。
显然，一般情况下矩阵A这三个性质均不满足。为了满足性质stochastic matrix，可以把全为0的行替换为e/ne/n，其中e为单位向量；同时为了满足性质不可约、非周期，需要做平滑处理：
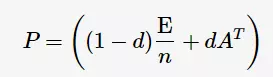
其中，d为 damping factor，常置为0与1之间的一个常数；E为单位阵。那么，式子（1）被改写为
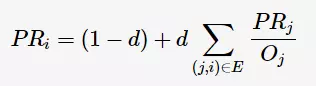
参考资料
[1] Bing Liu and Philip S. Yu, "The Top Ten Algorithms in Data Mining" Chapter 6.
往期回顾：
公众号后台回复关键词学习
回复 免费 获取免费课程
回复 直播 获取系列直播课
回复 Python 1小时破冰入门Python
回复 人工智能 从零入门人工智能
回复 深度学习 手把手教你用Python深度学习
回复 机器学习 小白学数据挖掘与机器学习
回复 贝叶斯算法 贝叶斯与新闻分类实战
回复 数据分析师 数据分析师八大能力培养
回复 自然语言处理 自然语言处理之AI深度学习
