作者:射命丸咲 Python 与 机器学习 爱好者
知乎专栏:https://zhuanlan.zhihu.com/carefree0910-pyml
个人网站:http://www.carefree0910.com
往期阅读:
机器学习综述
从零开始学人工智能(21)--数学 · CNN · 从 NN 到 CNN
从零开始学人工智能(22)--Python · 朴素贝叶斯(一)· 框架
从零开始学人工智能(23)--Python · 朴素贝叶斯(二)· MultinomialNB
从零开始学人工智能(24)--Python · 朴素贝叶斯(三)· GaussianNB
从零开始学人工智能(25)--Python · 朴素贝叶斯(四)· MergedNB
从零开始学人工智能(26)--Tensorflow · LinearSVM
从零开始学人工智能(27)--Python · SVM(一)· 感知机
GitHub 地址:https://github.com/carefree0910/MachineLearning/blob/master/Notebooks/SVM/zh-cn/LinearSVM.ipynb
=============正文如下===========
很多人(包括我)第一次听说 SVM 时都觉得它是个非常厉害的东西,但其实SVM 本身“只是”一个线性模型。只有在应用了核方法后,SVM 才会“升级”成为一个非线性模型
不过由于普遍说起 SVM 时我们都默认它带核方法,所以我们还是随大流、称 SVM 的原始版本为 LinearSVM。不过即使“只是”线性模型,这个“只是”也是要打双引号的——它依旧强大,且在许许多多的问题上甚至要比带核方法的 SVM 要好(比如文本分类)
感知机回顾
在进入正题之前,我们先回顾一下感知机,因为 LinearSVM 往简单来说其实就只是改了感知机的损失函数而已,而且改完之后还很像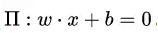
感知机模型只有和这两个参数,它们决定了一张超平面。感知机最终目的是使得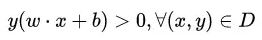 ,其中D是训练数据集、y只能取正负一
,其中D是训练数据集、y只能取正负一
训练方法则是梯度下降,其中梯度公式为:
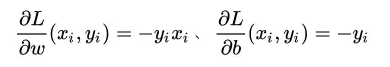
我们在实际实现时,采用了“极大梯度下降法”(亦即每次只选出使得损失函数最大的样本点来进行梯度下降)(注:这不是被广泛承认的称谓,只是本文的一个代称):
for _ in range(epoch):
# 计算 w·x+b
y_pred = x.dot(self._w) + self._b
# 选出使得损失函数最大的样本
idx = np.argmax(np.maximum(0, -y_pred * y))
# 若该样本被正确分类,则结束训练
if y[idx] * y_pred[idx] > 0:
break
# 否则,让参数沿着负梯度方向走一步
delta = lr * y[idx]
self._w += delta * x[idx]
self._b += delta
然后有理论证明,只要数据集线性可分,这样下去就一定能收敛
感知机的问题与 LinearSVM 的解决方案
由感知机损失函数的形式可知,感知机只要求样本被正确分类,而不要求样本被“很好地正确分类”。这就导致感知机弄出来的超平面(通常又称“决策面”)经常会“看上去很不舒服”:
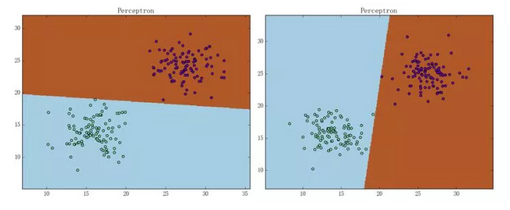
之所以看上去很不舒服,是因为决策面离两坨样本都太近了。从直观上来说,我们希望得到的是这样的决策面:
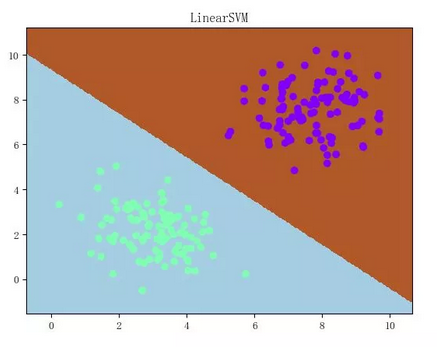
(之所以画风突变是因为 matplotlib 的默认画风变了,然后我懒得改了……)(喂
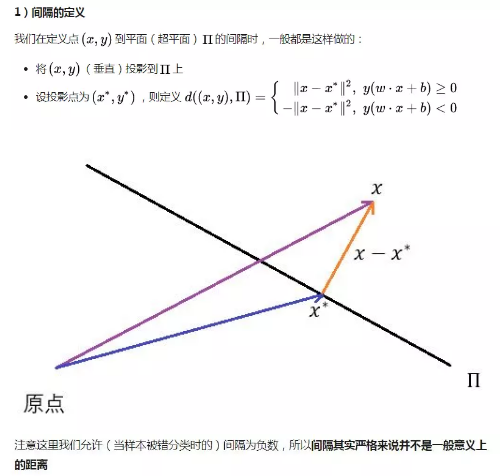
那么应该如何将这种理想的决策面的状态翻译成机器能够学习的东西呢?直观来说,就是让决策面离正负样本点的间隔都尽可能大;而这个“间隔”翻译成数学语言,其实就是简单的:

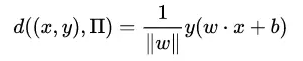
(文末会给出相应说明)
在有了样本点到决策面的间隔后,数据集到决策面的间隔也就好定义了:

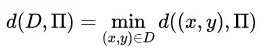




LinearSVM 的训练
【虽然比较简单,但是调优 LinearSVM 的训练这个过程是相当有启发性的事情。仍然是那句老话:麻雀虽小,五脏俱全。我们会先展示“极大梯度下降法”的有效性,然后会展示极大梯度下降法存在的问题,最后则会介绍如何应用 Mini-Batch 梯度下降法(MBGD)来进行训练】
为了使用梯度下降法,我们需要先求导。我们已知:
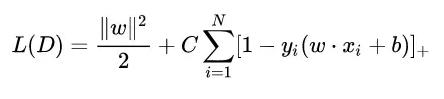
所以我们可以认为:


我们完全可以照搬感知机里的代码来完成实现(由于思路基本一致,这里就略去注释了):
import numpy as np class LinearSVM:
def __init__(self):
self._w = self._b = None
def fit(self, x, y, c=1, lr=0.01, epoch=10000):
x, y = np.asarray(x, np.float32), np.asarray(y, np.float32)
self._w = np.zeros(x.shape[1])
self._b = 0.
for _ in range(epoch):
self._w *= 1 - lr
err = 1 - y * self.predict(x, True)
idx = np.argmax(err)
# 注意即使所有 x, y 都满足 w·x + b >= 1
# 由于损失里面有一个 w 的模长平方
# 所以仍然不能终止训练,只能截断当前的梯度下降
if err[idx] <= 0:
continue
delta = lr * c * y[idx]
self._w += delta * x[idx]
self._b += delta
def predict(self, x, raw=False):
x = np.asarray(x, np.float32)
y_pred = x.dot(self._w) + self._b
if raw:
return y_pred
return np.sign(y_pred).astype(np.float32)
下面这张动图是该 LinearSVM 的训练过程:
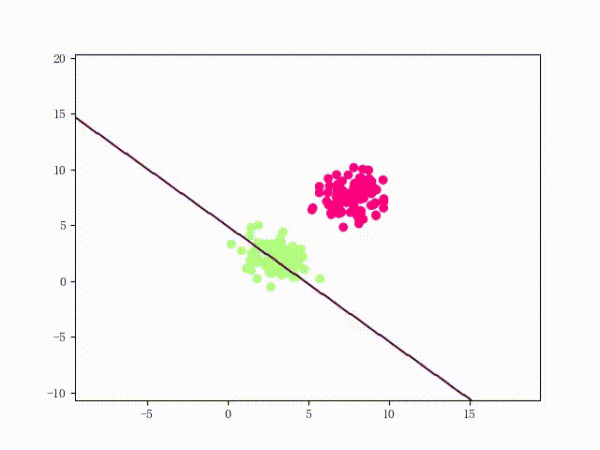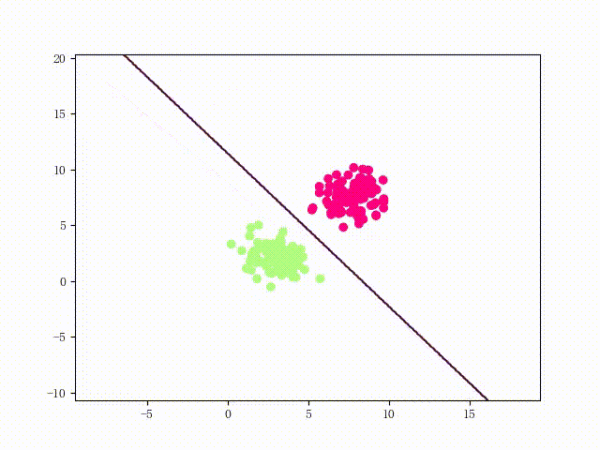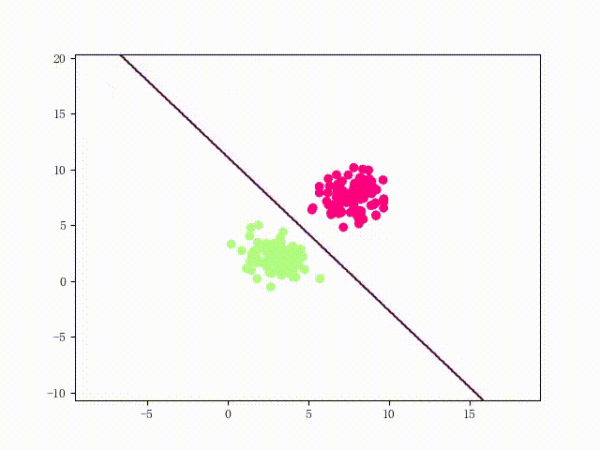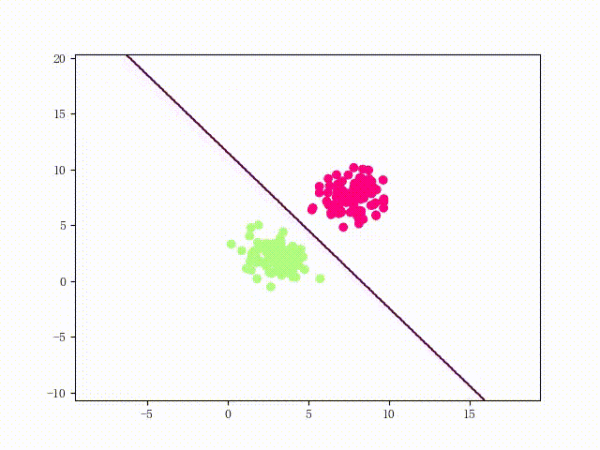
虽然看上去不错,但仍然存在着问题:
通过将正负样本点的“中心”从原点 (0, 0)(默认值)挪到 (5, 5)(亦即破坏了一定的对称性)并将正负样本点之间的距离拉近一点,我们可以复现这个问题:

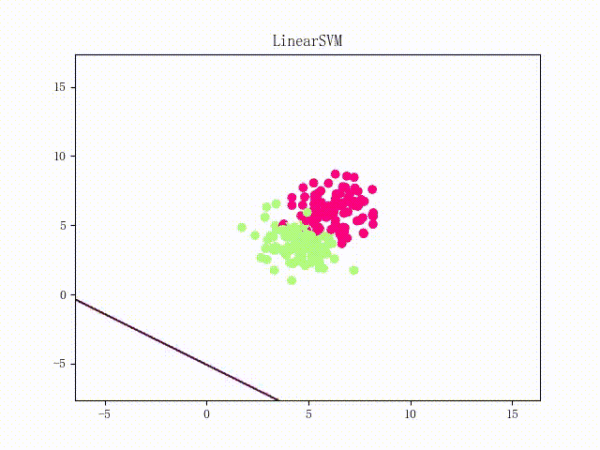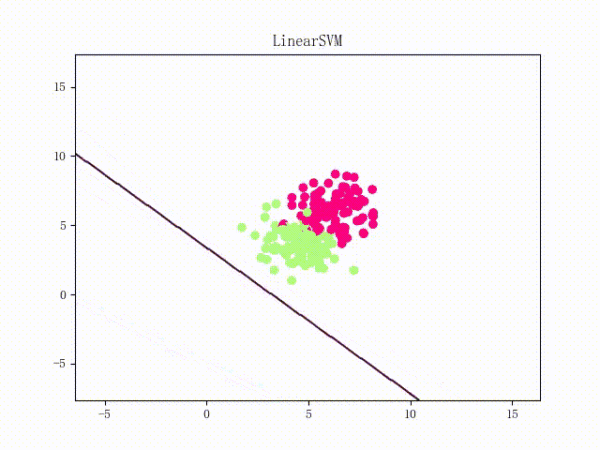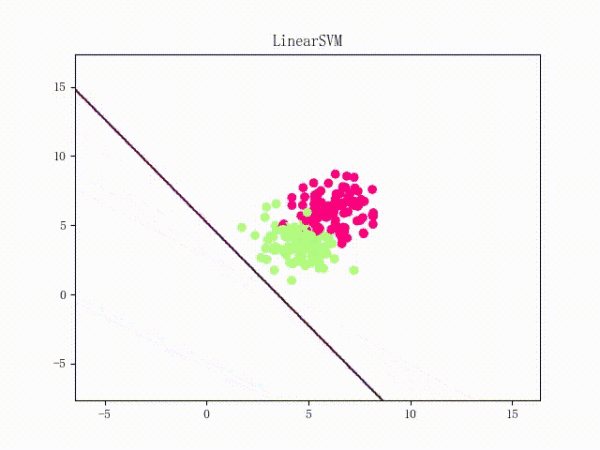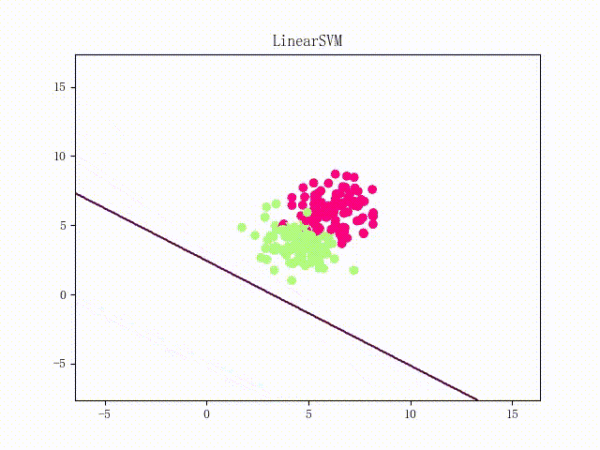
原理我不敢乱说,这里只提供一个牵强附会的直观解释:
专业的理论就留待专业的观众老爷补充吧 ( σ'ω')σ
然后解决方案的话,主要还是从改进随机梯度下降(SGD)的思路入手(因为极大梯度下降法其实就是 SGD 的特殊形式)。我们知道 SGD 的“升级版”是 MBGD、亦即拿随机 Mini-Batch 代替随机抽样,我们这里也完全可以依样画葫芦。以下是对应代码(只显示出了核心部分):
self._w *= 1 - lr# 随机选取 batch_size 个样本batch = np.random.choice(len(x), batch_size)x_batch, y_batch = x[batch], y[batch]err = 1 - y_batch * self.predict(x_batch, True)if np.max(err) <= 0: continue# 注意这里我们只能利用误分类的样本做梯度下降# 因为被正确分类的样本处、这一部分的梯度为 0mask = err > 0
delta = lr * c * y_batch[mask]
# 取各梯度平均并做一步梯度下降
self._w += np.mean(delta[..., None] * x_batch[mask], axis=0)
self._b += np.mean(delta)
这样的话,通常而言会比 SGD 要好
但是问题仍然是存在的:那就是它们所运用的梯度下降法都只是朴素的 Vanilla Update,这会导致当数据的 scale 很大时模型对参数极为敏感、从而导致持续的震荡(所谓的 scale 比较大,可以理解为“规模很大”,或者直白一点——以二维数据为例的话——就是横纵坐标的数值很大)。下面这张动图或许能提供一些直观:
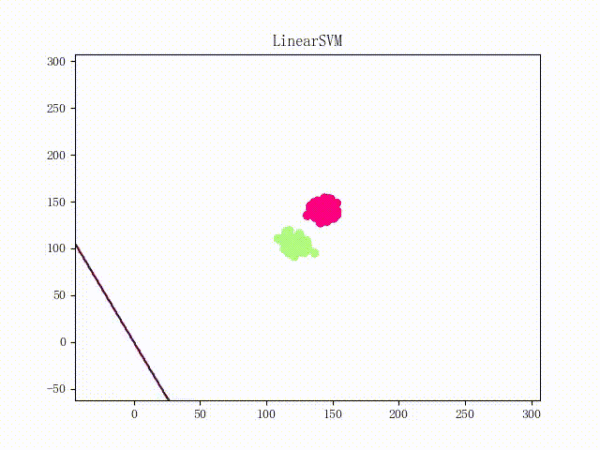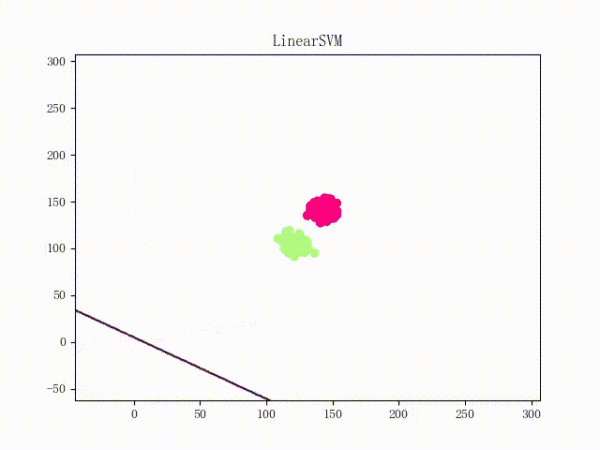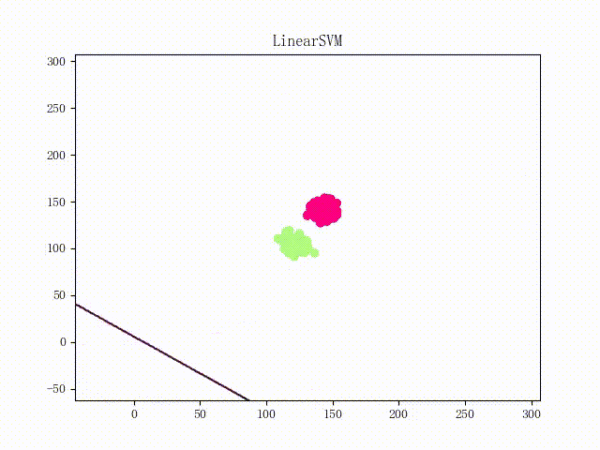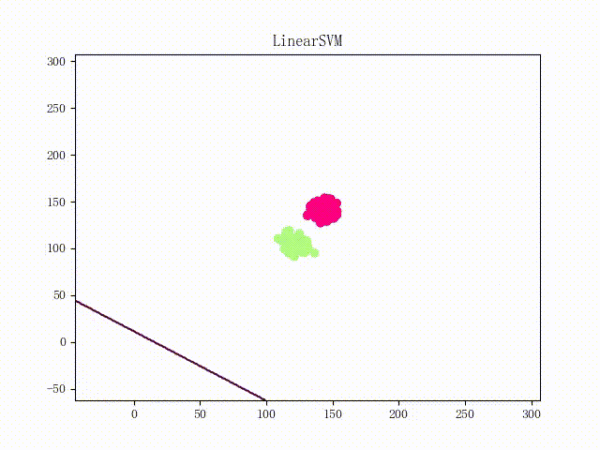
Again,原理我不敢乱说,所以只提供一个有可能对(更有可能错)(喂)的直观解释:
scale太大梯度很大蹦跶得很欢(什么鬼!)
专业的理论就留待专业的观众老爷补充吧 ( σ'ω')σ
解决方案的话,一个很直接的想法就是进行数据归一化:
 。事实证明这样做了之后,最基本的极大梯度下降法也能解决上文出现过的所有问题了
。事实证明这样做了之后,最基本的极大梯度下降法也能解决上文出现过的所有问题了
然后一个稍微“偷懒”一点的做法就是,用更好的梯度下降算法来代替朴素的 Vanilla Update。比如说 Adam 的训练过程将如下(这张动图被知乎弄得有点崩……将就着看吧 ( σ'ω')σ):

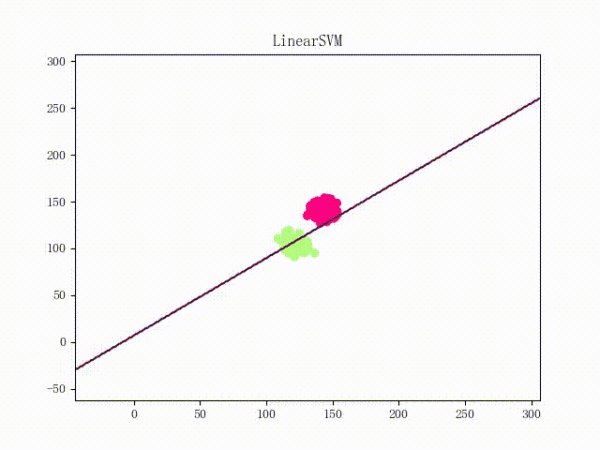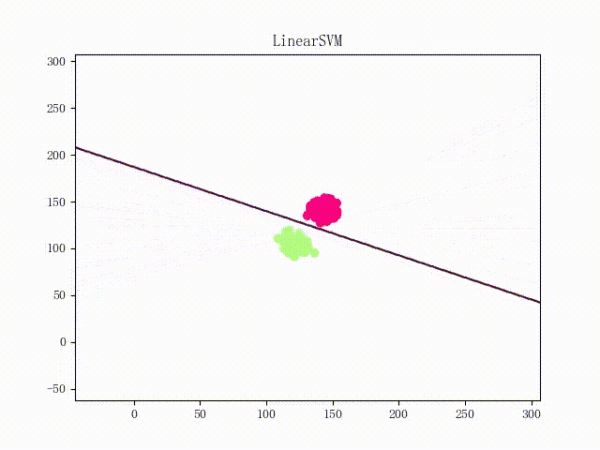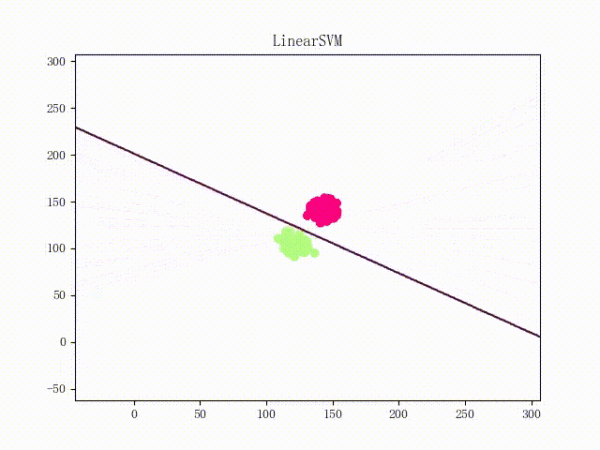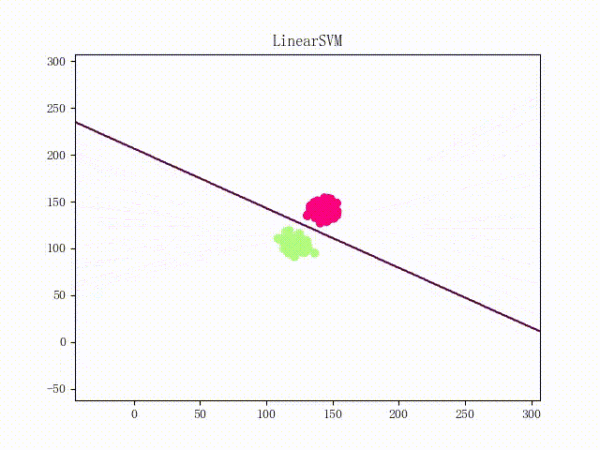
关于各种梯度下降算法的定义、性质等等可以参见这篇文章(http://www.carefree0910.com/posts/55a23cf0/),实现和在 LinearSVM 上的应用则可以参见这里和这里
相关数学理论
我们尚未解决的问题有三个,但这些问题基本都挺直观的,所以大体上不深究也没问题(趴:


这三个问题有一定递进关系,我们一个个来看


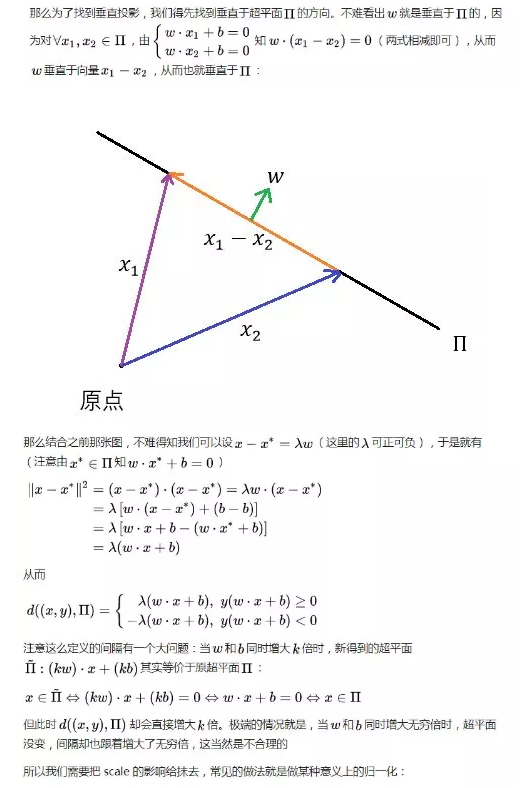

2)优化问题的转化的合理性

3)优化问题的等价性



4)LinearSVM 的对偶问题




然后最后的最后,请允许我不加证明地给出两个结论(因为结论直观且证明太长……):
下一篇文章我们则会介绍核方法,并会介绍如何将它应用到感知机和 SVM 上
希望观众老爷们能够喜欢~

公众号后台回复关键词学习
回复 人工智能 揭开人工智能的神秘面纱
回复 贝叶斯算法 贝叶斯算法与新闻分类
回复 机器学习 R&Python机器学习
回复 阿里数据 阿里数据系列课程
回复 Python Python机器学习案例实战
回复 Spark 征服Spark第一季
回复 kaggle 机器学习kaggle案例
回复 大数据 大数据系列视频
回复 数据分析 数据分析人员的转型
回复 数据挖掘 数据挖掘与人工智能
回复 机器学习 R&Python机器学习
回复 阿里数据 阿里数据系列课程
回复 R R&Python机器学习入门
