作者:射命丸咲 Python 与 机器学习 爱好者
知乎专栏:https://zhuanlan.zhihu.com/carefree0910-pyml
个人网站:http://www.carefree0910.com
往期阅读:
机器学习综述
从零开始学人工智能(17)--数学 · 神经网络(一)· 前向传导
从零开始学人工智能(18)--数学 · 神经网络(二)· BP(反向传播)
关于损失函数宽泛而准确的数学定义,我感觉我不会说得比 Wiki 更好,所以这一章主要还是介绍一些神经网络中常用的损失函数。然而即使把范围限制在 NN,如何选、为何选相应的损失函数仍然是一个不平凡的数学问题。囿于时间(和实力)、这一章讲的主要是几个损失函数的定义、直观感受和求导方法。
从名字上可以看出,损失函数是模型对数据拟合程度的反映,拟合得越差、损失函数的值就应该越大。同时我们还期望,损失函数在比较大时、它对应的梯度也要比较大,这样的话更新变量就可以更新得快一点。我们都接触过的“距离”这一概念也可以被用在损失函数这里,对应的就是最小平方误差准则(MSE):
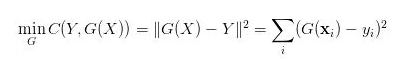
其中G是我们的模型、它根据输入矩阵X输出一个预测向量G(X)
这个损失函数的直观意义相当明确:预测值G(X)和真值Y的欧式距离越大、损失就越大,反之就越小。它的求导也是相当平凡的:
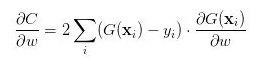
其中 w 是模型G中的一个待训练的参数
由于 MSE 比较简单、所以我们能够从一般意义上来讨论它。为便于理解,以下的部分会结合 NN 这个特定的模型来进行阐述。回顾 BP 算法章节中的式子:
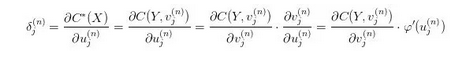
这里的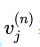 其实就是G(X)。在 NN 中,我们通过最后一层的 CostLayer 利用
其实就是G(X)。在 NN 中,我们通过最后一层的 CostLayer 利用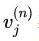 和真值Y得出一个损失、然后 NN 通过最小化这个损失来训练模型
和真值Y得出一个损失、然后 NN 通过最小化这个损失来训练模型
注意到上式的最后除了损失函数自身的导数以外、还有一项激活函数(https://en.wikipedia.org/wiki/Activation_function)的导数。事实上,结合激活函数来选择损失函数是一个常见的做法,用得比较多的组合有以下四个:
以上、大概讲了一些损失函数相关的基本知识。下一章的话会讲如何根据梯度来更新我们的变量、亦即会讲如何定义各种 Optimizers 以及会讲背后的思想是什么。可以想象会是一个相当大的坑……
希望观众老爷们能够喜欢~

公众号后台回复关键词学习
回复 人工智能 揭开人工智能的神秘面纱
回复 贝叶斯算法 贝叶斯算法与新闻分类
回复 机器学习 R&Python机器学习
回复 阿里数据 阿里数据系列课程
回复 Python Python机器学习案例实战
回复 Spark 征服Spark第一季
回复 kaggle 机器学习kaggle案例
回复 大数据 大数据系列视频
回复 数据分析 数据分析人员的转型
回复 数据挖掘 数据挖掘与人工智能
回复 机器学习 R&Python机器学习
回复 阿里数据 阿里数据系列课程
回复 R R&Python机器学习入门