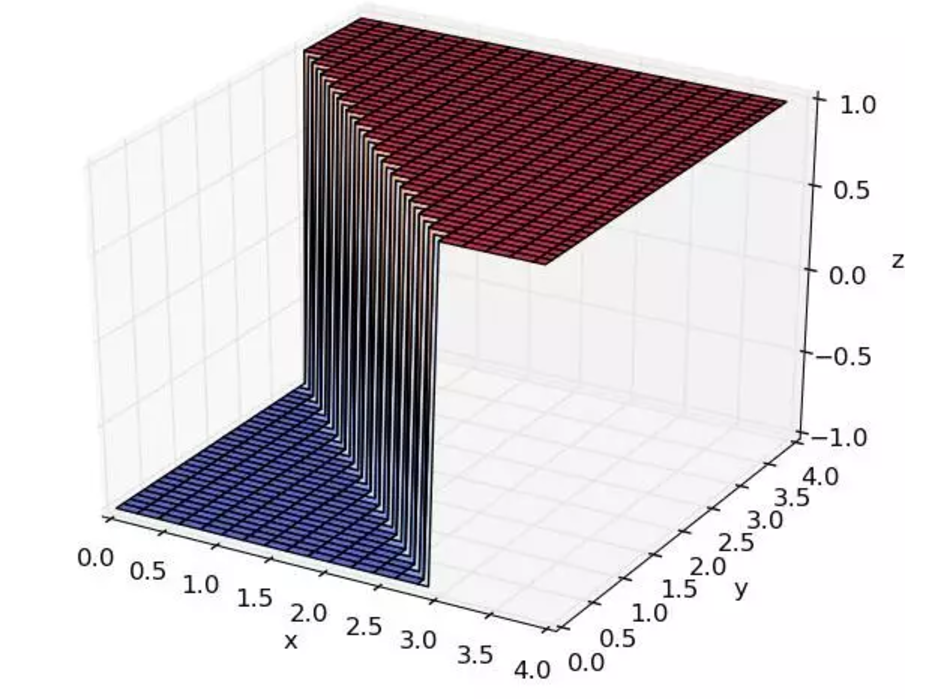
感知器PLA是一种最简单，最基本的线性分类算法（二分类）。其前提是数据本身是线性可分的。
模型可以定义为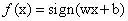，sign函数是阶跃函数，阈值决定取0或1。模型选择的策略，利用经验损失函数衡量算法性能，由于该算法最后得到一个分离超平面，所以损失函数可以定义为
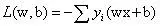，由于对于误分类点，yi和wx+b的正负属性相反，所以，所以加一个符号，来表征样例点与超平面的距离。
算法选择，最终的目标是求损失函数的最小值，利用机器学习中最常用的梯度下降GD或者随机梯度下降SGD来求解。
SGD算法的流程如下：输入训练集和学习率
1、初始化w0，b0，确定初始化超平面，并确定各样例点是否正确分类（利用yi和wx+b的正负性关系）；
2、随机在误分类点中选择一个样例点，计算L关于w和b在该点处的梯度值；
3、更新w，b，按照如下方向；
4、迭代运行，直到满足停止条件（限定迭代次数或者定义可接受误差最大值）；
如上所述，初值的选择，误分类点的选择顺序都影响算法的性能和运行时间。PLA是一个很基本的算法，应用场景很受限，只是作为一个引子来了解机器学习，后面有很多高级的算法，比如SVM和MLP，以及大热的deep learning，都是感知器的扩展。
对于PLA，还有一个对偶问题，此处，简单介绍一下对偶问题相关的知识。
对偶问题：
每一个线性规划问题，我们称之为原始问题，都有一个与之对应的线性规划问题我们称之为对偶问题。原始问题与对偶问题的解是对应的，得出一个问题的解，另一个问题的解也就得到了。并且原始问题与对偶问题在形式上存在很简单的对应关系：目标函数对原始问题是极大化,对对偶问题则是极小化。原始问题目标函数中的收益系数（优化函数中变量前面的系数）是对偶问题约束不等式中的右端常数,而原始问题约束不等式中的右端常数则是对偶问题中目标函数的收益系数；原始问题和对偶问题的约束不等式的符号方向相反；原始问题约束不等式系数矩阵转置后即为对偶问题的约束不等式的系数矩阵；原始问题的约束方程数对应于对偶问题的变量数,而原始问题的变量数对应于对偶问题的约束方程数；对偶问题的对偶问题是原始问题。总之他们存在着简单的矩阵转置，系数变换的关系。当问题通过对偶变换后经常会呈现许多便利，如约束条件变少、优化变量变少，使得问题的求解证明更加方便计算可能更加方便。
对偶问题中，此处将w和b看成是x和y的函数，w和b可表示为，ni表示更新次数，模型
，算法流程如下：输入训练集，学习率
1、；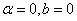
2、随机选取误分类点对，并更新计算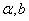，具体更新，依据上面的表达式；
3、直至没有误分类点，停止计算，返回相应的参数；
原始问题和对偶问题都是严格可收敛的，在线性可分的条件下，一定可以停止算法运行，会达到结果，存在多个解。
如果线性不可分，可以利用口袋算法，每次迭代更新错误最小的权值，且规定迭代次数。口袋算法基于贪心的思想。他总是让遇到的最好的线拿在自己的手上。。。 就是我首先手里有一条分割线wt，发现他在数据点(xn,yn)上面犯了错误，那我们就纠正这个分割线得到wt+1,我们然后让wt与wt+1遍历所有的数据，看哪条线犯的错误少。如果wt+1犯的错误少，那么就让wt+1替代wt，否则wt不变。 那怎样让算法停下来呢？？——–我们就 自己规定迭代的次数 由于口袋算法得到的线越来越好（PLA就不一定了，PLA是最终结果最好，其他情况就说不准了），所以我们就 自己规定迭代的次数 。
感知机python实现代码
#coding = utf-8
import numpy as np
import matplotlib.pyplot as plt
class showPicture:
def __init__(self,data,w,b):
self.b = b
self.w = w
plt.figure(1)
plt.title('Plot 1', size=14)
plt.xlabel('x-axis', size=14)
plt.ylabel('y-axis', size=14)
xData = np.linspace(0, 5, 100)
yData = self.expression(xData)
plt.plot(xData, yData, color='r', label='y1 data')
plt.scatter(data[0][0],data[0][1],s=50)
plt.scatter(data[1][0],data[1][1],s=50)
plt.scatter(data[2][0],data[2][1],marker='x',s=50,)
plt.savefig('2d.png',dpi=75)
def expression(self,x):
y = (-self.b - self.w[0]*x)/self.w[1]
return y
def show(self):
plt.show()
class perceptron:
def __init__(self,x,y,a=1):
self.x = x
self.y = y
self.w = np.zeros((x.shape[1],1))
self.b = 0
self.a = 1
def sign(self,w,b,x):
result = 0
y = np.dot(x,w)+b
return int(y)
def train(self):
flag = True
length = len(self.x)
while flag:
count = 0
for i in range(length):
tmpY = self.sign(self.w,self.b,self.x[i,:])
if tmpY*self.y[i]<=0:
tmp = self.y[i]*self.a*self.x[i,:]
tmp = tmp.reshape(self.w.shape)
self.w = tmp +self.w
self.b = self.b + self.y[i]
count +=1
if count == 0:
flag = False
return self.w,self.b
#原始数据
data = [[3,3],[4,3],[1,1]]
xArray = np.array([3,3,4,3,1,1])
xArray = xArray.reshape((3,2))
yArray = np.array([1,1,-1])
#感知机计算权值
myPerceptron = perceptron(x=xArray,y=yArray)
weight,bias = myPerceptron.train()
#画图
picture = showPicture(data,w=weight,b=bias)
picture.show()