神经网络：NN 入门

浏览: 2756

（这里是本章会用到的 Jupyter Notebook 地址）

将感知机应用于多分类任务

我们之前在 支持向量机：感知机 里面介绍感知机时，用的是这么一个公式：y_{pred}=w\cdot x+b，然后样本中的y要求只能取\pm1。这在二分类任务时当然没问题，但是到多分类时就会有些问题。虽说我们是可以用各种方法让二分类模型去做多分类任务的，不过那些方法普遍都比较麻烦。为了让我们的模型天然适应于多分类任务，我们通常会将样本中的y取为\text{One-Hot}向量，亦即

  • y\in第 k 类\Leftrightarrow y除了第 k 位为 1 以外、其余位都是 0

此时我们的感知机就会变成这样（以 N 个拥有 n 维特征的样本的 K 分类任务为例；为简洁，省略了偏置量 b）：

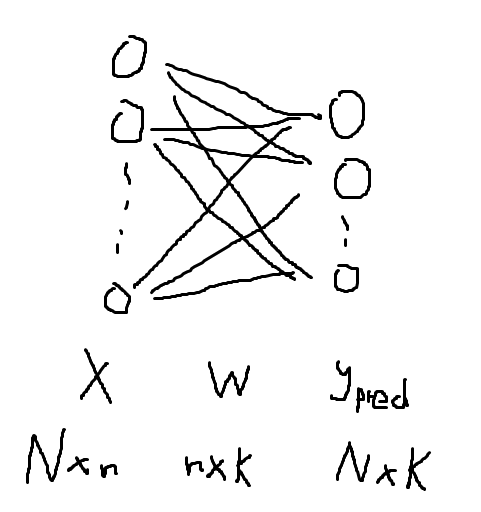
Untitled.png

（看在我纯鼠绘的份上原谅我画得那么丑吧 | ω･`)）

此时模型的表示会变为y_{pred}=Xw。注意到我们原来输出的是一个数，在改造后输出的则是一个 K 维向量。也正因此，我们不能简单地沿用之前定义的损失函数（L=|yy_{pred}|_+）、而应该定义一个新的损失函数

由于我们的目的是让模型输出的向量y_{pred}和真实的（\text{One-Hot}）标签向量y“越近越好”，而“距离”是一个天然的衡量“远近”的东西，所以用欧氏距离来定义损失函数是比较自然的。具体而言，我们可以把损失函数定义为L=\|y_{pred}-y\|^2在有了损失之后就可以求导了。需要指出的是，虽然我接下来写的公式看上去挺显然，但由于我们进行的是矩阵求导工作，所以它们背后真正的逻辑其实没那么显然。有兴趣的观众老爷可以看看这篇文章，这里就先直接给出结果，细节会附在文末：

\frac{\partial L}{\partial w}=\frac{\partial y_{pred}}{\partial w}\frac{\partial L}{\partial y_{pred}}=2X^T(y_{pred}-y)

利用它，我们就能写出相应的梯度下降训练算法了：

import numpy as np



class MultiPerceptron:

    def __init__(self):

        # 注意这里的 self._w 将来会是（n x K 的）矩阵

        self._w = None

        

    def fit(self, x, y, lr=1e-3, epoch=1000):

        x, y = np.asarray(x, np.float32), np.asarray(y, np.float32)

        # x.shape[1] 即为 n、y.shape[1] 即为 K

        self._w = np.zeros([x.shape[1], y.shape[1]])

        for _ in range(epoch):

            # 依公式进行梯度下降

            y_pred = x.dot(self._w)

            dw = 2 * x.T.dot(y_pred - y)

            self._w -= lr * dw

    

    def predict(self, x):

        # 依公式计算模型输出向量

        y_pred = np.asarray(x, np.float32).dot(self._w)

        # 预测类别时对输出的 K 维向量用 argmax 即可

        return np.argmax(y_pred, axis=1).astype(np.float32)

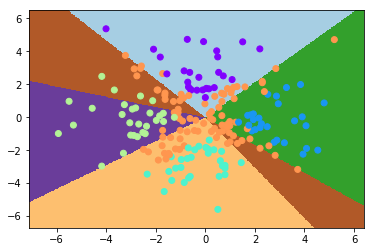
该模型的表现如下：

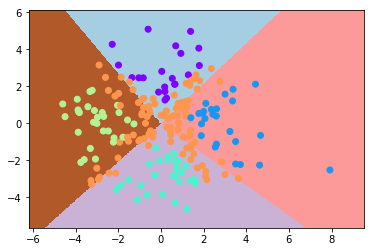
download.png

此时正确率为 50% 左右。可以看到模型输出中基本没有对角线上的那一类（而这一类恰恰是最多的），这是因为将感知机拓展为多类模型并不会改变它是线性模型的本质、所以其分类效果仍然是线性的，从而它无法拟合出对角线那一类的边界

从感知机到神经网络

那么怎样才能把感知机变成一个非线性的模型呢？我在 支持向量机：核方法 中曾介绍过核方法这看上去非常高端大气的东西，这篇文章的话就主要介绍另一种思路。具体而言：

  • 现有的感知机只有两层（输入层和输出层），是否能多加一些层？
  • 核方法从直观上来说，是利用满足一定条件的核函数将样本空间映射到高维空间；如果我放宽条件、使用一些一般的比较好的函数，是否也能起到一定的效果？

基于这两个想法，我们可以把上面画过的感知机模型的结构弄成下图这种结构：

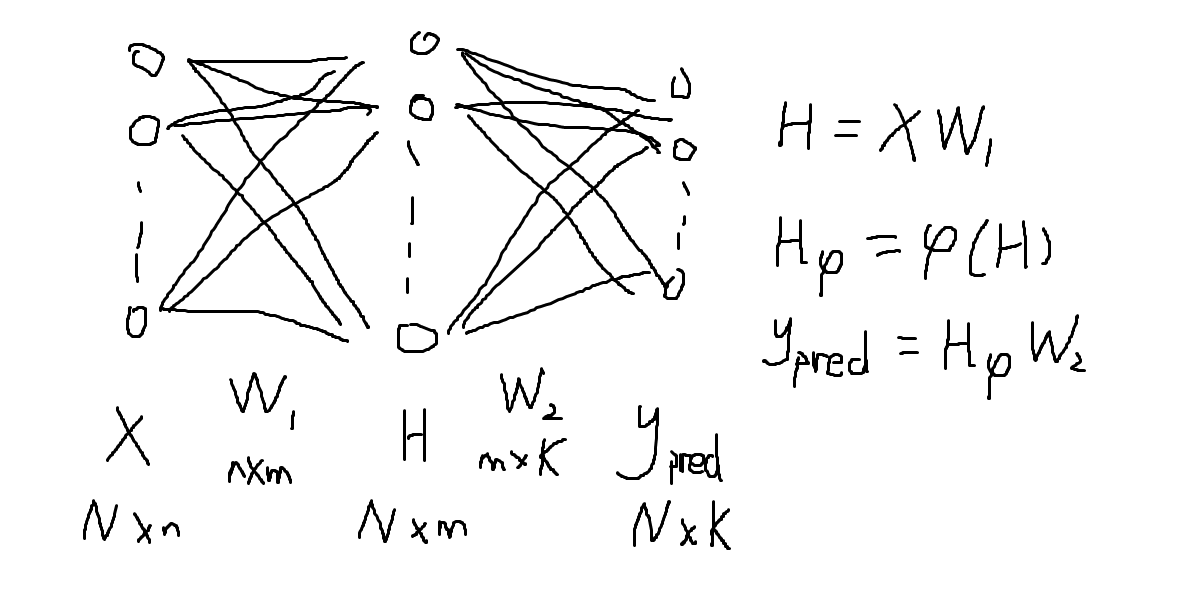
Untitled2.png

其中，我们通常（假设共有 N 个样本）：

  • 称\varphi为“激活函数”
  • 称w_1和w_2权值矩阵
  • 称往中间加的那些层为“隐藏层”；为简洁，此后我们讨论时认为只加了一层隐藏层，多层的情况会在下一篇文章讨论
  • 称图中每个圈儿为“神经元”。以上图为例的话：
    • 输入层有 n 个神经元
    • 隐藏层有 m 个神经元
    • 输出层有 K 个神经元

然后，激活函数其实就是上文所说的一般的比较好的函数；常用激活函数的相关介绍我会附在文末，这里就暂时认定激活函数为我们之前在 SVM 处就见过的 ReLU，亦即认定\varphi(x)=|x|_+=\max(0, x)

这个结构看上去很强大，但求导求起来却也会麻烦不少（损失函数仍取L=\|y_{pred}-y\|^2）：

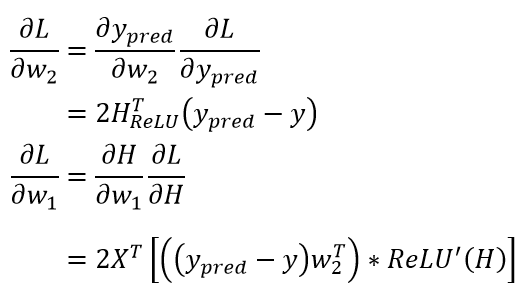
Untitled3.png

其中，“ * ”表示乘法的 element-wise 操作（或者专业一点的话，叫 Hadamard 乘积）、ReLU'表示对 ReLU 函数进行求导。由于当\varphi为 ReLU 时我们有\varphi(x)=|x|_+=\max(0, x)，所以其求导也是非常简单的：

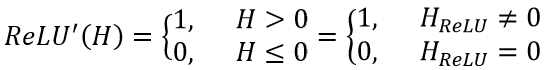
Untitled4.png

利用这两个求导公式，相应的梯度下降算法是比较好实现的：

class NaiveNN:

    def __init__(self):

        # 这里的 self._ws 将会是一个存储着两个权值矩阵的列表

        self._ws = None

        

    @staticmethod

    def relu(x):

        # 利用 numpy 相应函数直接写出 ReLU 的实现

        return np.maximum(0, x)

    

    # hidden_dim 即为隐藏层神经元个数 m

    def fit(self, x, y, hidden_dim=32, lr=1e-5, epoch=1000):

        input_dim, output_dim = x.shape[1], y.shape[1]

        # 随机初始化权值矩阵

        self._ws = [

            np.random.random([input_dim, hidden_dim]),

            np.random.random([hidden_dim, output_dim])

        ]

        # 定义一个列表存储训练过程中的损失

        losses = []

        for _ in range(epoch):

            # 依公式算出各个值

            h = x.dot(self._ws[0]); h_relu = NaiveNN.relu(h)

            y_pred = h_relu.dot(self._ws[1])

            # 利用 np.linalg.norm 算出损失

            losses.append(np.linalg.norm(y_pred - y, ord="fro"))

            # 依公式算出各个梯度

            d1 = 2 * (y_pred - y)

            dw2 = h_relu.T.dot(d1)

            dw1 = x.T.dot(d1.dot(self._ws[1].T) * (h_relu != 0))

            # 走一步梯度下降

            self._ws[0] -= lr * dw1; self._ws[1] -= lr * dw2

        # 把诸模型损失返回

        return losses

    

    def predict(self, x):

        h = x.dot(self._ws[0]); h_relu = NaiveNN.relu(h)

        # 用 argmax 预测类别

        return np.argmax(h_relu.dot(self._ws[1]), axis=1)

该模型的表现如下：

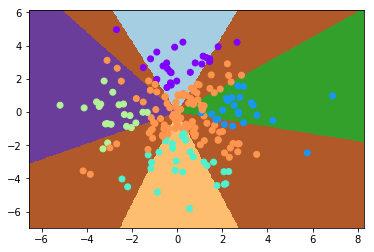
download (1).png

download (2).png

虽然还是比较差（准确率 70% 左右），但已经有模有样了

使用 Softmax + Cross Entropy

可能已经有观众老爷发现，我把上面这个模型的训练速率的默认值调到了10^{-5}，这是因为稍大一点的训练速率都会使模型直接爆炸。这是因为我们没有对最后一层做变换、而是直接简单粗暴地用了y_{pred}=H_{ReLU}w_2。这导致最终模型的输出很有可能突破天际，这当然不是我们想看到的

考虑到标签是\text{One-Hot}向量，换一个角度来看的话，它其实也是一个概率分布向量。那么我们是否可以将模型的输出也变成一个概率向量呢？事实上，我们耳熟能详的 Softmax 正是干这活儿的，具体而言，假设现在有一个向量y=(y_1,y_2,...,y_K)^T，那么就有：

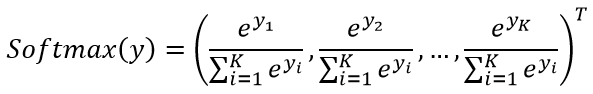
Untitled5.png

不难看出这是个概率向量，且从直观上来看颇为合理。在真正应用 Softmax 会有一个提高数值稳定性的小技巧，细节会附在文末，这里就暂时按下

于是在应用了 Softmax 之后，我们模型的输出就变成一个概率向量了。诚然此时仍然能用欧氏距离作为损失函数，不过一种普遍更优的做法是使用 Cross Entropy（交叉熵）作为损失函数。具体而言，两个随机变量y（真值）、y_{pred}（预测值）的交叉熵为：

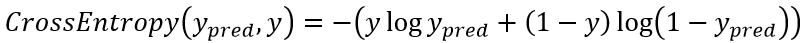
Untitled6.png

交叉熵拥有如下两个性质：

  • 当真值为 0（y=0）时，交叉熵其实就化为了-\log(1-y_{pred})，此时预测值越接近 0、交叉熵就越接近 0，反之若预测值趋于 1、交叉熵就会趋于无穷
  • 当真值为 1（y=1）时，交叉熵其实就化为了-\log y_{pred}，此时预测值越接近 1、交叉熵就越接近 0，反之若预测值趋于 0、交叉熵就会趋于无穷

所以拿交叉熵作为损失函数是合理的。真正应用交叉熵时同样会有提高数值稳定性的小技巧——在 log 里面放一个小值以避免出现 log 0 的情况：

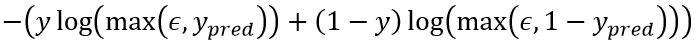
Untitled7.png

在加了这两个东西之后，我们就要进行求导了。虽说求导过程比较繁复，但令人惊喜的是，最终结果和之前的结果是几乎一致的，区别只在于倍数（推导过程参见文末）：

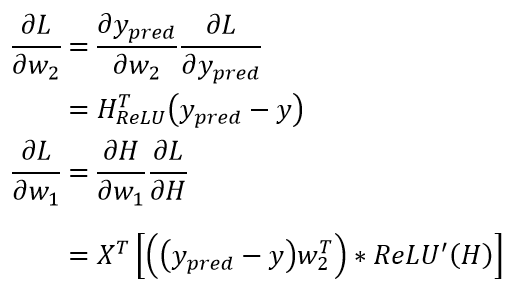
Untitled8.png

所以相应的实现也几乎一致：

class NN:

    def __init__(self, ws=None):

        self._ws = ws

        

    @staticmethod

    def relu(x):

        return np.maximum(0, x)

    

    @staticmethod

    def softmax(x):

        exp_x = np.exp(x - np.max(x, axis=1, keepdims=True))

        return exp_x / np.sum(exp_x, axis=1, keepdims=True)

    

    @staticmethod

    def cross_entropy(y_pred, y_true):

        return -np.average(

            y * np.log(np.maximum(y_pred, 1e-12)) +

            (1 - y) * np.log(np.maximum(1 - y_pred, 1e-12))

        )

    

    def fit(self, x, y, hidden_dim=4, lr=1e-3, epoch=1000):

        input_dim, output_dim = x.shape[1], y.shape[1]

        if self._ws is None:

            self._ws = [

                np.random.random([input_dim, hidden_dim]),

                np.random.random([hidden_dim, output_dim])

            ]

        losses = []

        for _ in range(epoch):

            h = x.dot(self._ws[0]); h_relu = NN.relu(h)

            y_pred = NN.softmax(h_relu.dot(self._ws[1]))

            losses.append(NN.cross_entropy(y_pred, y))

            d1 = y_pred - y

            dw2 = h_relu.T.dot(d1)

            dw1 = x.T.dot(d1.dot(self._ws[1].T) * (h_relu != 0))

            self._ws[0] -= lr * dw1; self._ws[1] -= lr * dw2

        return losses

    

    def predict(self, x):

        h = x.dot(self._ws[0]); h_relu = NaiveNN.relu(h)

        # 由于 Softmax 不影响 argmax 的结果，所以这里直接 argmax 即可

        return np.argmax(h_relu.dot(self._ws[1]), axis=1)

该模型的表现如下：

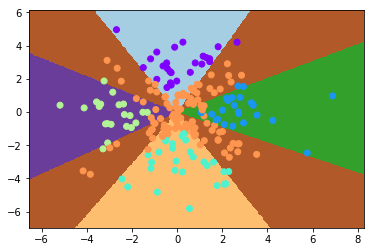
download (3).png

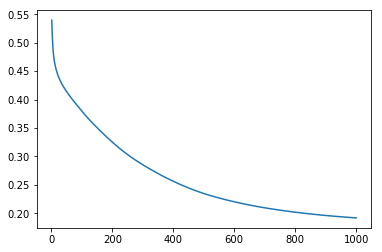
download (4).png

虽说仍不完美，但它和不使用 Softmax + Cross Entropy 的模型相比，有这么两个优势：

  • 训练速率可以调得更大（10^{-4}vs10^{-5}），这意味着该模型没那么容易爆炸（什么鬼）
  • 模型的训练更加稳定，亦即每次训练出来的结果都差不多。反观之前的模型，我所给出的模型表现其实是精挑细选出来的；在一般情况下，其表现其实是类似于这样的（这告诉我们，一个好的结果很有可能是由无数 sb 结果堆积出来的……）：

download (5).png

相关数学理论

1）常见激活函数

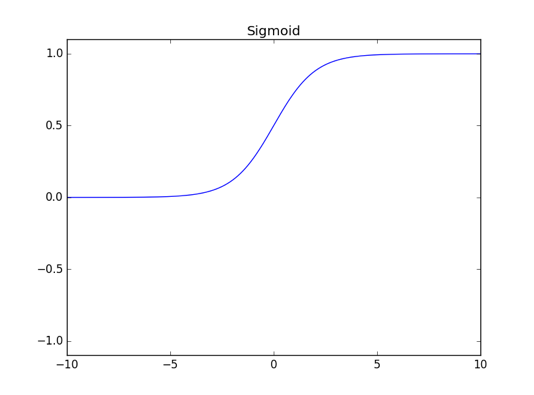
A、Sigmoid：

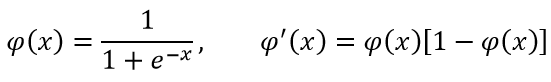
Untitled13.png

p2.png

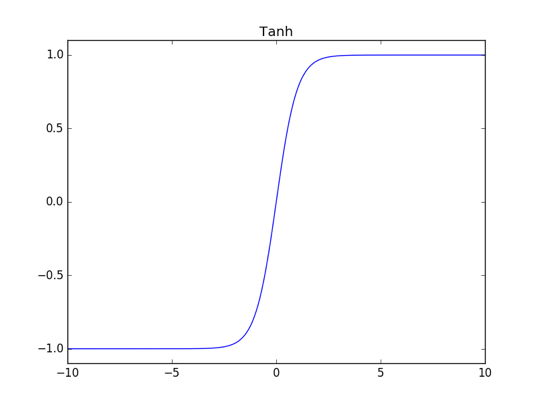
B、Tanh：

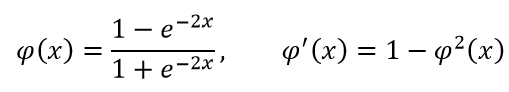
Untitled14.png

p3.png

C、ReLU：

Untitled15.png

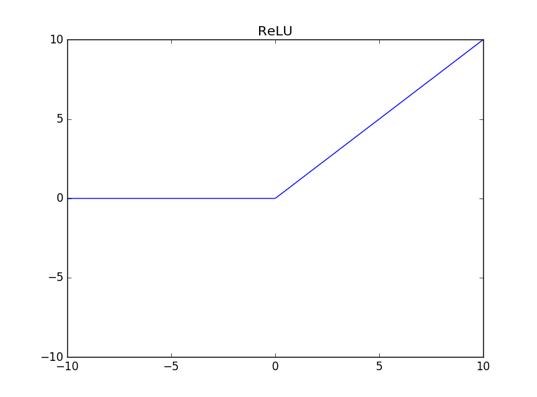
p4.png

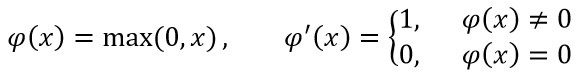
D、ELU：

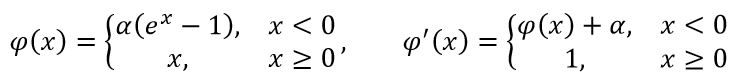
Untitled16.png

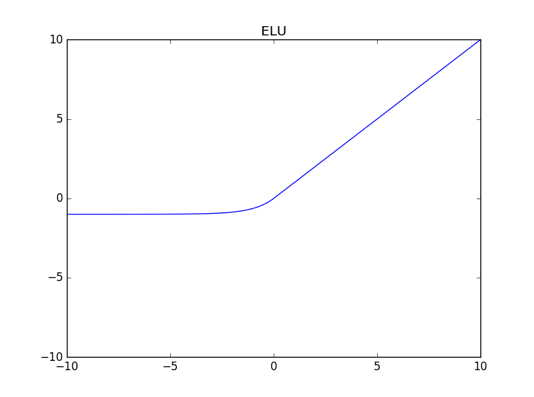
p5.png

E、Softplus：

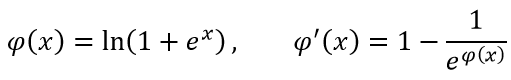
Untitled17.png

p6.png

以及最近出了一个叫 SELU 的激活函数，论文整整有 102 页……感兴趣的观众老爷们可以参见[1706.02515] Self-Normalizing Neural Networks

2）神经网络中导数的计算

为了书写简洁，接下来我们会用矩阵求导的技巧来进行计算；不过如果觉得看着太绕的话，建议还是参照这篇文章、依定义逐元素求导（事实上我也经常绕不过来……）

由简入繁，我们先来看多分类感知机的求导过程。我们之前曾说过多分类感知机可以写成y_{pred}=Xw、其中（假设有 N 个样本）：

  • X是N\times n的矩阵
  • w是n\times K的矩阵、从而y_{pred}是N\times K的矩阵
  • 损失L=\|y_{pred}-y\|^2是一个N\times1的向量

不少人在尝试求 \frac{\partial L}{\partial w}时，会以为需要用向量对矩阵求导的法则，虽然不能说是错的，却可能会把问题变复杂。事实上，多分类感知机的本质是对随机向量\bold{x}的某个采样x进行预测，X只不过是一个多次采样后产生的样本矩阵而已。因此，多分类感知机的本质其实是\tilde{y}=W\bold x、其中：

  • x是n\times1的向量
  • W是K\times n的权值矩阵（事实上，W=w^T）、从而\tilde{y}是K\times1的随机向量
  • 损失L=\|\tilde{y}-y\|^2是一个数

于是求导过程就化简为标量对矩阵的求导了：

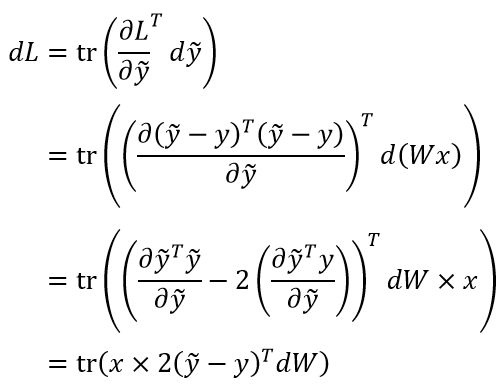
Untitled9.png

由此可知\frac{\partial L}{\partial W}=2(\tilde y-y)x^T。在求出这个特殊情形之后，应该如何把它拓展到样本矩阵的情形呢？虽说严谨的数学叙述会比较麻烦（需要用到矩阵的向量化【又称“拉直”】之类的），但我们可以这样直观地理解：

  • 当样本从一个变成多个时，权值矩阵的导数理应是从一个变成多个的加总

因此我们只需利用矩阵乘法完成这个加总的过程即可。注意到我们可以直观地写出：

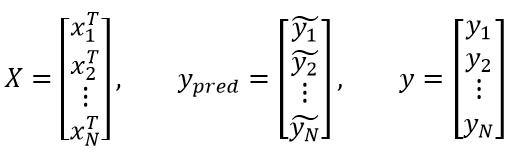
Untitled10.png

且“加总”即为\frac{\partial L}{\partial W}=\sum_{i=1}^N2(\tilde y_i-y_i)x_i^T，从而我们可以直观地写出\frac{\partial L}{\partial W}=2(y_{pred}-y)^TX注意到我们有w=W^T，所以就有\frac{\partial L}{\partial w}=2X^T(y_{pred}-y)单隐藏层的、没有应用 Softmax + Cross Entropy 的神经网络的推导是类似的，此时：

  • h=W_1x，其中x、W_1、h的形状分别是n\times1、m\times n、m\times 1
  • \tilde y=W_2\varphi(h)，其中\varphi是 ReLU，W_2、\tilde y的形状分别是K\times m、K\times1
  • L=(\tilde y-y)^T(\tilde y-y)

于是

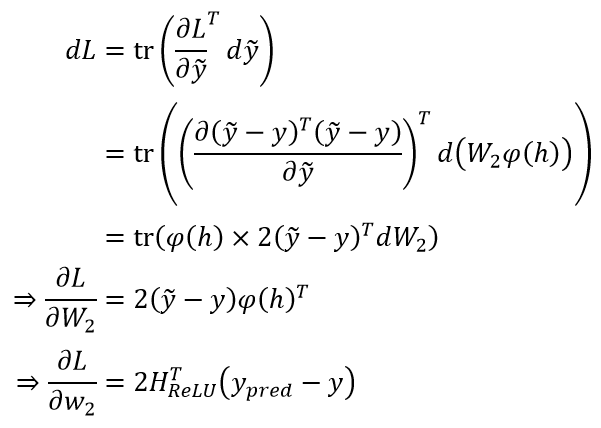
Untitled11.png

以及

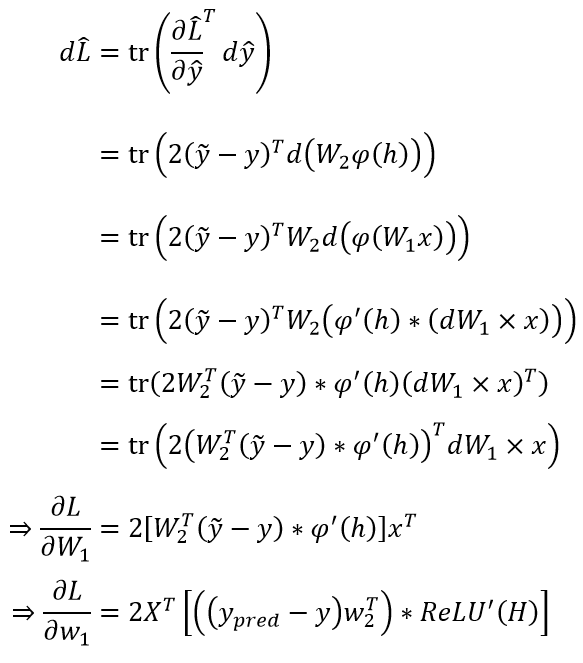
Untitled12.png

3）Softmax + Cross Entropy

在应用了 Softmax + Cross Entropy 之后，上面求导过程中受影响的其实只有\frac{\partial L}{\partial\tilde y}这一项，所以只需看这一项如何变化的即可

在展开讨论之前，需要先做一些符号约定（假设原模型输出向量为\tilde y=(\tilde y_1, \tilde y_2,...,\tilde y_K)^T）：

  • 令\phi=(\phi_1,\phi_2,...,\phi_K)^T，其中\phi_i=e^{\tilde y_i}
  • 设 Softmax 后的模型输出向量为\hat y=(\hat y_1,\hat y_2,...\hat y_K)^T，那么依定义就有

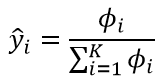
Untitled18.png

  • 设交叉熵对应的损失函数为\hat L，则有\hat L=-[y\log \hat y+(1-y)\log(1-\hat y)]

从而可知d\hat L=\text{tr}\left(\frac{\partial\hat L}{\partial\hat y}^Td\hat y\right)，其中

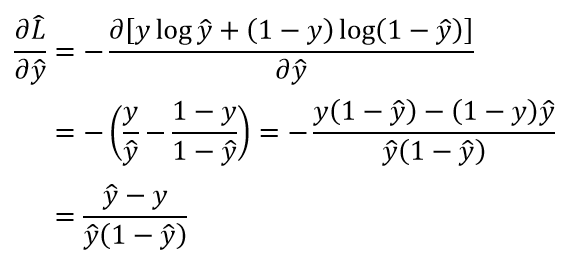
Untitled19.png

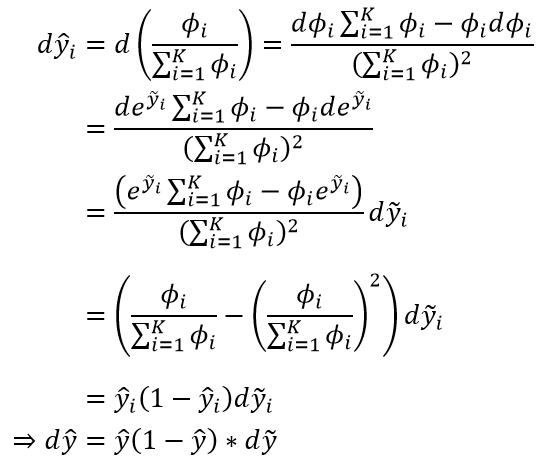
Untitled20.png

亦即

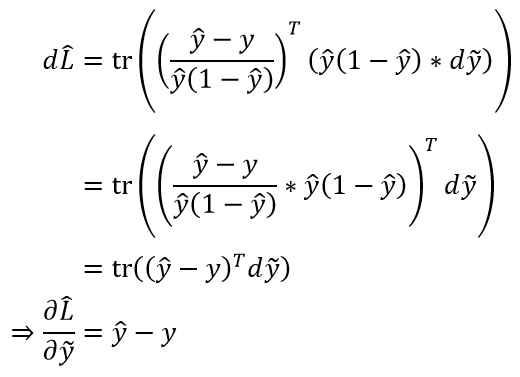
Untitled21.png

本文我们主要讨论了如何将感知机应用于多分类任务，并通过直观的思想——加深感知机的层次和应用激活函数来得到更强力的模型（神经网络）。此外，我们还讨论了如何应用 Softmax + Cross Entropy 来让模型变得更加稳定。然而我们讨论的范围仍局限于单隐藏层和 ReLU 激活函数，下一篇文章我们会介绍更一般的情形，并通过一种方式来直观说明神经网络的强大

希望观众老爷们能够喜欢~

推荐 5
梁勇 秦汉 ylxklmls zeekvfu 掌羊
本文由 射命丸咲 创作，采用 知识共享署名-相同方式共享 3.0 中国大陆许可协议 进行许可。
转载、引用前需联系作者，并署名作者且注明文章出处。
本站文章版权归原作者及原出处所有 。内容为作者个人观点， 并不代表本站赞同其观点和对其真实性负责。本站是一个个人学习交流的平台，并不用于任何商业目的，如果有任何问题，请及时联系我们，我们将根据著作权人的要求，立即更正或者删除有关内容。本站拥有对此声明的最终解释权。

5 个评论

梁勇

梁勇

有几个图片看不到。最近要爱好者社区连载你的系列文章啊，给力。有深度。
2017-07-11 18:36
射命丸咲

射命丸咲 回复 梁勇

Σ( ° △ °|||)︴我这就去改！
2017-07-11 21:27
射命丸咲

射命丸咲 回复 梁勇

终于改完了，幸好当初没有把备份的图片删掉……
以及多谢梁勇老师抬爱~我会继续努力把文章写好的！(ง๑ •̀_•́)ง
2017-07-11 21:40
ylxklmls

ylxklmls

收藏啊
2017-07-12 13:53
射命丸咲

射命丸咲 回复 ylxklmls

(´▽`ʃƪ)
2017-07-12 16:23

要回复文章请先登录或注册