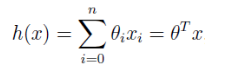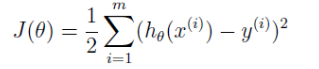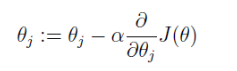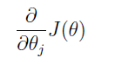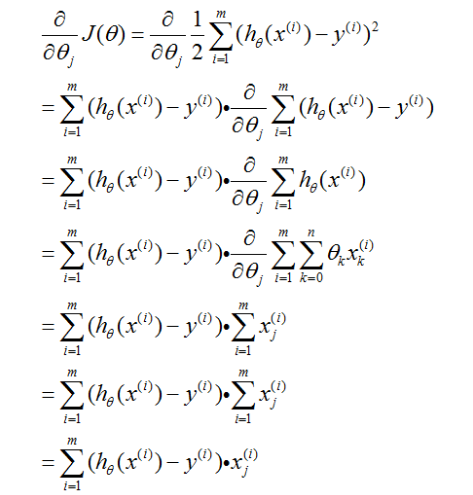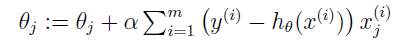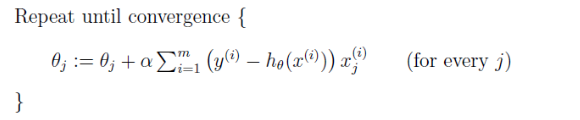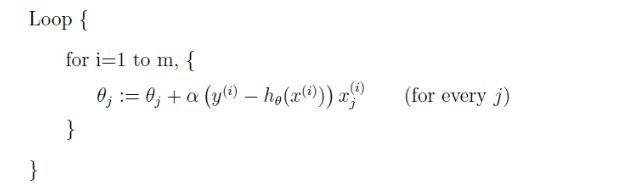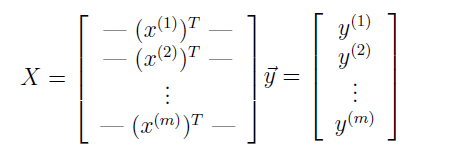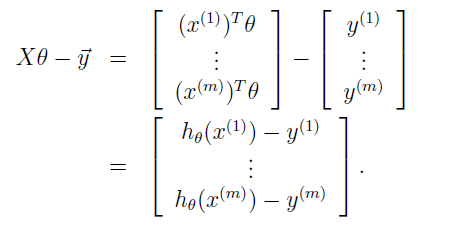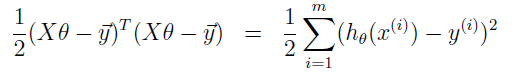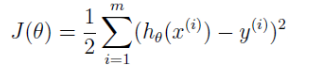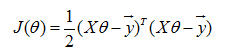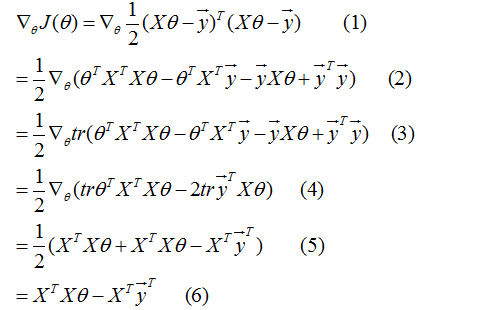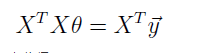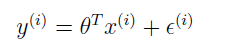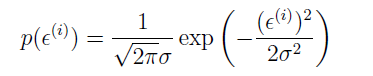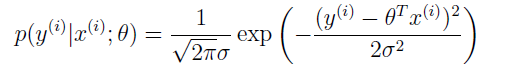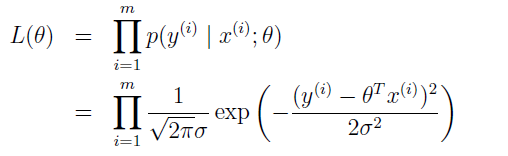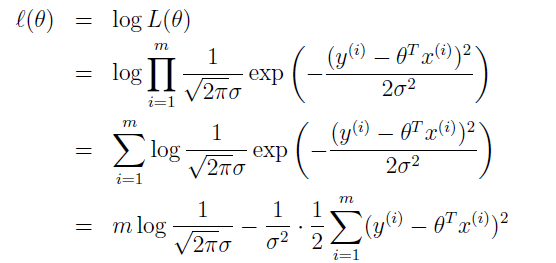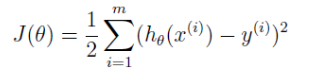问题:给定一个数据集,自变量是房子面积和房间数,目标变量是房子价格,当来了个新房子,知道其房子面积和房间数,如何预测价格?
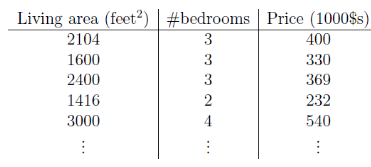
解:我们是想找到一个公式,能够根据面积和房间数算出价格,这个公式不仅能在训练集上畅行无阻,在新数据上也要能尽量准确。还不知道这三个变量是什么关系,不妨假定价格是面积和房间数的线性函数吧。
假设价格是面积和房间数的线性函数,x1 和 x2 分别表示已知的面积和房间个数,θ 是权重参数,h(x) 是预测的房子价格。
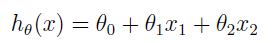
符号简化后如下:
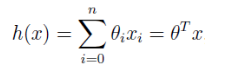
现在,x 和 θ 都是长度为 n+1 的向量。
得到了参数 θ,我们就能根据新的面积和房间数计算价格,那么,怎么根据当前的训练数据集得到 θ 呢? θ 值肯定不是随便给,那要满足什么要求呢?
毫无疑问,要想准确预测新数据,得出的 θ 最起码应该保证在训练集上预测房价准确些,怎么才算准确些呢?计算出的价格与真实的价格应尽量接近。计算价格和实际价格的差距以损失函数来表示。
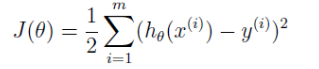
我们最终选择的 θ 要使 J(θ) 最小,对 θ 就这个要求 。
好,现在我们的目标就是要找到使 J(θ) 最小的 θ 。
找 θ 有两种方法,一种是梯度下降法,是搜索算法,先给 θ 赋个初值,然后再根据使 J(θ) 更小的原则对 θ 进行修改,直到最小 θ 收敛,J(θ) 达到最小,也就是不断尝试;另外一种是矩阵求导法,要使 J(θ) 最小,就对 θ 求导,使导数等于 0,求得 θ。
1、梯度下降法
要找到使 J(θ) 最小的 θ 向量,首先给 θ 向量赋个初值,然根据梯度下降法不断更新 θ 向量的每个元素。
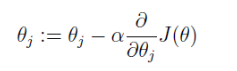
其中 α 是步长,也称学习率,步子小了收敛慢,步子大了容易跳过收敛值,然后在收敛值附近震荡。
然后的问题就是求导:
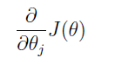
把上面 J(θ) 公式代入求导即可,如下公式所示。
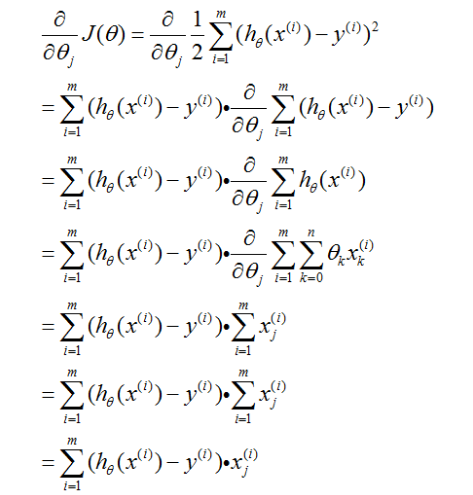
所以 θ 的更新公式为:
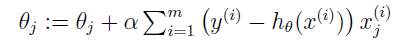
完整算法如下:
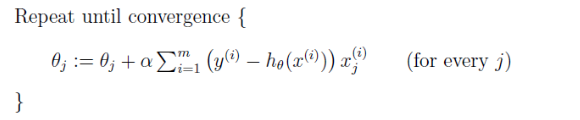
可以看到在对 θ 的更新中用到的是 ∂J(θ)/∂θj,这种算法在每一步计算都要用到完整的数据集,被称为批梯度下降。我们这里的线性回归最优化问题只有一个全局最优,没有其它局部最优。所以这里的梯度下降会一直收敛到全局最小。其实这里的 J(θ) 是凸二次函数。
除了批梯度下降,还有一种是随机梯度下降。
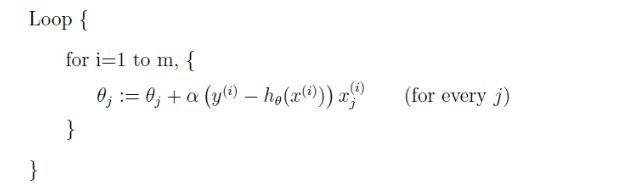
每遇到一个训练数据都要更新下参数。对于批梯度下降来说,每执行一步,都要遍历完整个训练集,当 m 很大时就是一个非常耗费时间的操作。但对于随机梯度下降来说就很快,每扫描一个训练数据都能进一步。所以,随机梯度下降的 θ 经常比批梯度下降更快地趋近最优值。尽管随机梯度下降可能不会收敛到最优值,但参数 θ 会保持在 J(θ) 最小值附近震荡,实践中最小值最近的大多数值就够使了,所以当训练集很大时,随机梯度下降是更常用的。
2、矩阵求导法
首先定义:
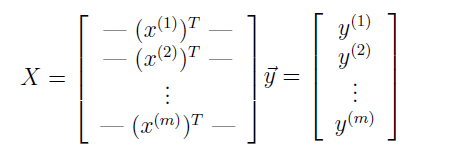
再由 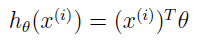 得:
得:
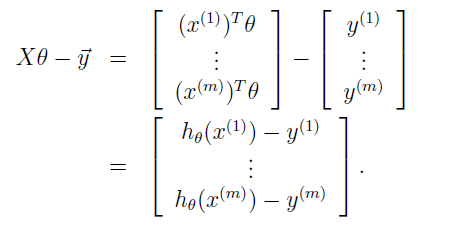
由 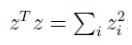 得:
得:
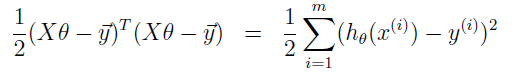
因为:
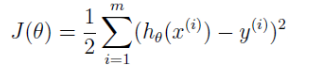
所以:
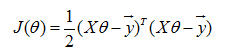
然后就是求 J(θ) 关于 θ 的导数,并使其等于 0,最后就可以求出 θ。J(θ) 求导过程如下。
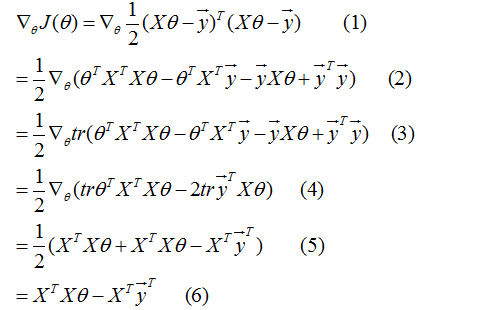
上面的推导过程看着很复杂,但稍微耐心看下每一步,就会觉得顺理成章了。具体每一步的推导依据可参考 http://cs229.stanford.edu/notes/cs229-notes1.pdf 第 11 页。
为最小化 J(θ),我们置公式(6)为 0,得:
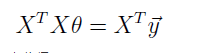
由此得:
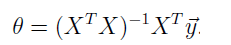
至此,解题完毕,给了两种方法。
我们再来谈下,为什么说最小均方损失函数是个合理的选择?我们会发现最小均方损失函数是符合一些概率假设的。
假设因变量和自变量是通过如下方程联系起来的:
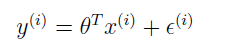
其中 ε(i) 是一个误差项,表示未捕捉到的有效因子,或者随机噪声。假定 ε(i) 是独立同分布的,符合均值为 0,方差为 σ2 的高斯分布,那么的概率密度函数为:
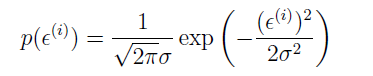
那么 y(i) 的概率密度为:
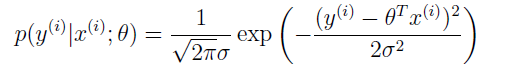
注意这里符号 p(y(i)|x(i);θ) 表示给定 x(i) 和参数 θ 后 y(i) 的分布。不能写成 p(y(i)|x(i),θ),因为 θ 不是个随机变量。
数据的概率为 p(y|X;θ),把它看作是 θ 的函数,即似然函数。
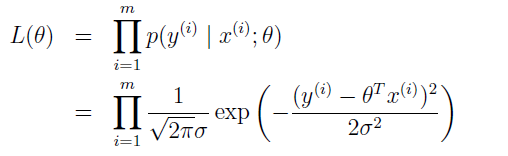
最大似然函数的奥义就是通过选择 θ 使得数据出现的概率尽可能得大。即寻找 θ 来最大化 L(θ)。
直接最大化 L(θ) 有难度,我们也可以最大化 L(θ) 的一些严格递增函数。比如,最大化 L(θ) 的 log 函数。
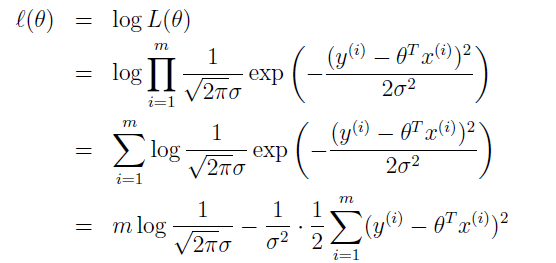
注意到,这跟最小化 J(θ) 是一样的。
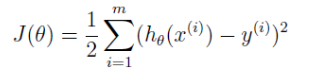
所以,在之前对数据的概率假设下,最小化均方回归跟寻找最大似然函数的 θ 是一样的。尽管概率假设对于最小均方来说是个非常合理的过程,当然也可以通过其他假设来推导出这个结果。
注意到上面的讨论中,θ 的选择跟方差 σ2 无关,即使方差 σ2 未知,θ 也能得到同样的结果。后面我们讨论指数分布簇和一般线性模型时会再次用到这个事实。